நாற்கரம்

நான்கு பக்கங்களைக் கொண்ட ஒரு பல்கோணம் நாற்கரம் அல்லது நாற்பக்கல் (quadrilateral) எனப்படும். மிகவும் பொதுமைப்படுத்தப்பட்ட நாற்கோணம் நான்கு சமனற்ற பக்கங்களைக் கொண்டது. $A$, $B$, $C$ and $D$ என்ற நான்கு உச்சிகளைக்கொண்ட நாற்கரம் $◻ABCD$ எனக் குறிக்கப்படுகிறது.

எளிய நாற்கரம் ABCD இன் உட்கோணங்களின் கூடுதல் 360 பாகைகள், அதாவது,

$\mathrm{\angle }A+\mathrm{\angle }B+\mathrm{\angle }C+\mathrm{\angle }D=360^{\circ }.$ ஒரு n-கோணியின் உட்கோணங்களின் கூடுதலுக்கான வாய்பாடு (n − 2) × 180° இல் n = 4 எனப் பதிலிட இம்மதிப்பு கிடைக்கும்

நாற்கர வகைகள்

நாற்கரங்கள் எளிமையானவையாக (தன்னைத் தானே வெட்டிக்கொள்ளாதவை) அல்லது சிக்கலானவையாக (தன்னைத் தானே வெட்டிக்கொள்கிற) இருக்கலாம்.

எளிமையான நாற்கரங்கள்

எளிமையான நாற்கரங்கள் குவிந்த நாற்கரங்களாகவோ அல்லது குழிந்த நாற்கரங்களாகவோ இருக்கக் கூடும். குவிந்த நாற்கரங்கள் பின்வரும் வகைகளாகப் பிரிக்கப்படும்:

குவிந்த நாற்கரங்கள்

• சரிவகம் (Trapezium): ஒரு சோடி எதிர்ப் பக்கங்கள் ஒன்றுக்கொன்று இணையானவை.

• இருசமபக்க சரிவகம் (Isosceles trapezium): ஒரு சோடி எதிர்ப் பக்கங்கள் இணையானவையாகவும், மற்ற இரண்டு பக்கங்களும் சமனானவையாகவும் இருக்கும். அடிக்கோணங்கள் இரண்டும் கோணங்கள் சமனானவையாகும்.

• இணைகரம் (Parallelogram): இரண்டு சோடி எதிர்ப்பக்கங்களும் ஒன்றுக்கொன்று இணையானவை; எதிர்ப் பக்கங்கள் சமனானவை; எதிர்க் கோணங்கள் சமனானவை.

• பட்டம்: இரண்டு சோடி அயல் பக்கங்கள் இரு வேறு சம நீளங்கள் கொண்டவை. இதனால் ஒரு சோடி எதிர்க் கோணங்கள் சமனானவை. மூலை விட்டங்கள் செங்கோணத்தில் ஒன்றையொன்று வெட்டும்.

• சாய்சதுரம் (Rhombus): நான்கு பக்கங்களும் ஒன்றுக்கொன்று சமனானவை. எதிர்ப் பக்கங்கள் ஒன்றுக்கொன்று இணையானவை, எதிர்க் கோணங்களும் ஒன்றுக்கொன்று சமனானவை. மூலைவிட்டங்கள் செங்கோணத்தில் சமகூறாக வெட்டுகின்றன.

• செவ்வகம் (Rectangle):எதிர்ப் பக்கங்கள் சம நீளம் கொண்டவை. ஒவ்வொரு கோணமும் செங்கோணமாகும். இதனால் எதிர்ப் பக்கங்கள் இணையானவை. மூலைவிட்டங்கள் செங்கோணத்தில் ஒன்றையொன்று சம துண்டங்களாக வெட்டுகின்றன.

• சதுரம் (square) (ஒழுங்கான நாற்கரங்கம்): நான்கு பக்கங்களும் சம நீளம் கொண்டவை. ஒவ்வொரு கோணமும் செங்கோணமாகும். இதனால் எதிர்ப் பக்கங்கள் இணையானவை. மூலைவிட்டங்கள் செங்கோணத்தில் ஒன்றையொன்று சம துண்டங்களாக வெட்டுகின்றன.

• வட்ட நாற்கரம் (Cyclic quadrilateral): நான்கு உச்சிகளும் ஒரு வட்டத்தின் பரிதியில் அமைந்திருப்பன.

• தொடுகோட்டு நாற்கரம் (Tangential quadrilateral): நான்கு பக்கங்களும் உள்ளே வரையப்பட்ட வட்டமொன்றின் தொடுகோடுகளாகும்.

• இருமைய நாற்கரம் (Bicentric quadrilateral): முன் குறிப்பிட்ட இரண்டுமாக இருக்கும்.

குழிந்த நாற்கரங்கள்

குழிந்த நாற்கரத்தில் ஒரு உட்கோணம் 180° விட அதிகமாக இருக்கும். மேலும் இரண்டு மூலைவிட்டங்களில் ஒன்று நாற்கரத்துக்கு வெளிப்புறத்தில் இருக்கும்.

சிக்கலான நாற்கரங்கள்

தன்னைத்தானே வெட்டிக்கொள்ளும் நாற்கரம், சிக்கலான நாற்கரம் எனப்படும். இது குறுக்கு-நாற்கரம் என்றும் அழைக்கப்படும். ஒரு குறுக்கு நாற்கரத்தின் குறுக்குக்கு ஒரே பக்கத்தில் அமையும் (இடப்புறம் அல்லது வலப்புறம்) நான்கு உட்கோணங்களின் (2 குறுங்கோணம், 2 பின்வளை கோணம்) கூடுதல் 720° ஆக இருக்கும்.

• குறுக்கு சரிவகம்: ஒரு சோடி அடுத்தில்லாத பக்கங்களை இணையாகக் கொண்ட குறுக்கு நாற்கரம்.
• எதிர் இணைகரம்: ஒவ்வொரு சோடி அடுத்தில்லாத பக்கங்களும் சமநீளமுள்ளவையாகக் கொண்ட குறுக்கு நாற்கரம்.
• குறுக்கு செவ்வகம்: ஒரு செவ்வகத்தின் இரு எதிர்ப்பக்கங்களையும் இரு மூலைவிட்டங்களையும் கொண்ட குறுக்கு நாற்கரம்.
• குறுக்கு சதுரம்: இரு பக்கங்கள் செங்கோணத்தில் வெட்டிக்கொள்ளும் குறுக்கு செவ்வகம்.

குறுக்கு இருசமபக்கச் சரிவகம்	எதிர் இணைகரம்	குறுக்கு செவ்வகம்	குறுக்கு சதுரம்

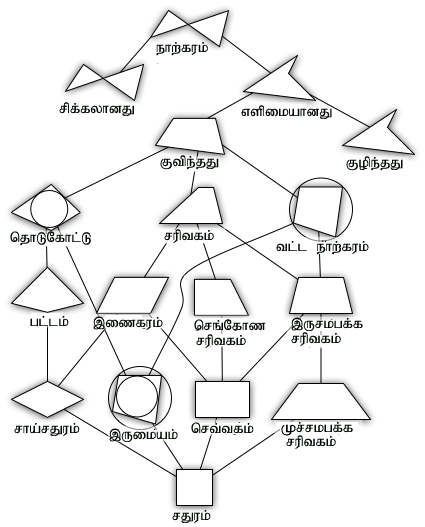
பெயரிடல் வகைப்பாடு

நாற்கரங்களின் பெயரிடல் வகைப்பாட்டைக் (taxonomic classification) கீழேயுள்ள வரைபு காட்டுகின்றது. கீழுள்ள வடிவங்கள் மேலுள்ள வடிவங்களின் சிறப்பு நிலைகளாகும்.

குவிந்த நாற்கரத்தின் பரப்பளவு

ஒரு குவிந்த செவ்வகத்தின் பரப்பளவு காண்பதற்கு பல வாய்பாடுகள் உள்ளன. எடுத்துக்கொள்ளப்படும் குவிந்த நாற்கரம் ABCD இன் பக்கங்கள்: வார்ப்புரு:Math; பரப்பளவு வார்ப்புரு:Math. 　

முக்கோணவியல் வாய்பாடுகள்

$K=\frac{pq}{2}\sin \theta ,$ வார்ப்புரு:Math, வார்ப்புரு:Math செவ்வகத்தின் மூலைவிட்டங்களின் நீளங்கள்; அவற்றுக்கு இடைப்பட்ட கோணம் வார்ப்புரு:Math.

செங்குத்து மூலைவிட்ட நாற்கரமாக இருந்தால் (எ.கா. சாய்சதுரம், சதுரம், பட்டம் போன்றவை)), பரப்பளவின் இவ்வாய்பாடு பின்னுள்ளபடி சுருங்கும்:

$K=\frac{pq}{2}$ (வார்ப்புரு:Math = வார்ப்புரு:Math, வார்ப்புரு:Math = வார்ப்புரு:Math).

இருநடுக்கோடுகளின் வாயிலாகப் பரப்பளவின் வாய்பாடு:

$K=mn\sin \phi ,$ இருநடுக்கோடுகளின் நீளங்கள் வார்ப்புரு:Math and வார்ப்புரு:Math; அவற்றுக்கு இடைப்பட்ட கோணம் வார்ப்புரு:Math.

குறுக்கு நாற்கரமல்லாதவற்றுக்கு கீழுள்ள இரு வாய்பாடுகள் பயன்படும்:

$K=\frac{1}{2}\sqrt{p^2{q}^2-[(d-a\cos A)(d-c\cos D)-ac\sin A\sin D{]}^2}$ (வார்ப்புரு:Math, வார்ப்புரு:Math, வார்ப்புரு:Math பக்கங்கள்; வார்ப்புரு:Math, வார்ப்புரு:Math கோணங்கள்)

$K=\frac{a\sin A(d-c\cos D)+(d-a\cos A)c\sin D}{2}$ (வார்ப்புரு:Math பக்கங்கள்; வார்ப்புரு:Math கோணங்கள்)

நாற்கரம் சரிவகமாக இருந்தால் வார்ப்புரு:Nobreak ஆகும். எனவே பரப்பளவின் வாய்பாடு கீழுள்ளவாறு சுருங்கும்:

$K=\frac{a+c}{2}d\sin A$

பிரெட்ஷ்ணைடரின் வாய்பாடு, நாற்கரத்தின் பரப்பளவை அதன் பக்கங்கள், இரு எதிர்கோணங்கள் வாயிலாகத் தருகிறது:

$\begin{array}{cc}K& =\sqrt{(s-a)(s-b)(s-c)(s-d)-\frac{1}{2}abcd[1+\cos (A+C)]}\\ & =\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\left[{\cos }^2\left(\frac{A+C}{2}\right)\right]}\end{array}$

இதில், வார்ப்புரு:Math, வார்ப்புரு:Math, வார்ப்புரு:Math, வார்ப்புரு:Math நான்கும் நாற்கரத்தின் பக்கங்கள்; வார்ப்புரு:Math அரைச்சுற்றளவு; வார்ப்புரு:Math, வார்ப்புரு:Math இரு எதிர்கோணங்கள். வார்ப்புரு:Math ஆக இருந்தால், நாற்கரம் வட்ட நாற்கரமாகும். அதன் பரப்பளவின் வாய்பாடு பிரம்மகுப்தரின் வாய்பாடு ஆகச் சுருங்கும்..

பக்கங்கள் வார்ப்புரு:Math, வார்ப்புரு:Math பக்கங்களுக்கு இடைப்பட்ட கோணம் வார்ப்புரு:Math; வார்ப்புரு:Math, வார்ப்புரு:Math பக்கங்களுக்கு இடைப்பட்ட கோணம் வார்ப்புரு:Math எனில் பரப்பளவின் வாய்பாடு:

$K=\frac{ad}{2}\sin A+\frac{bc}{2}\sin C.$

வட்ட நாற்கரமாக இருந்தால் இதே வாய்பாடு பின்வருமாறு அமையும்:

$K=\frac{ad+bc}{2}\sin A.$ (வார்ப்புரு:Math => sinC=sin(180-A)=sinA)

இணைகரத்தின் இரு சோடி எதிர்ப்பக்கங்களும் கோணங்களும் சமம் என்பதால், பரப்பளவின் வாய்பாடு: $K=ab\cdot \sin A.$ (வார்ப்புரு:Math; வார்ப்புரு:Math, வார்ப்புரு:Math)

நாற்கரத்தின் பக்கங்கள், மூலைவிட்டங்கள் வெட்டிக்கொள்ளும் கோணம் வார்ப்புரு:Math (வார்ப்புரு:Math, வார்ப்புரு:Math ஆக இருக்கக் கூடாது) வாயிலாக பரப்பளவு:

$K=\frac{|\tan \theta |}{4}\cdot |a^2+c^2-b^2-d^2|.$

இணைகரத்துக்கு இந்த வாய்பாடு:

$K=\frac{|\tan \theta |}{2}\cdot |a^2-b^2|.$ (வார்ப்புரு:Math, வார்ப்புரு:Math)

வார்ப்புரு:Math, வார்ப்புரு:Math, வார்ப்புரு:Math, வார்ப்புரு:Math ஆகிய நான்கு பக்கங்கள் வாயிலாக மற்றொரு வாய்பாடு:

$K=\frac{\sqrt{((a^2+c^2)-2x^2)((b^2+d^2)-2x^2)}}{2}\sin \phi$

இதில், வார்ப்புரு:Math ஆனது மூலைவிட்டங்களின் நடுப்புள்ளிகளுக்கு இடைப்பட்ட தூரம்; வார்ப்புரு:Math என்பது இருநடுக்கோடுகளுக்கு இடைப்பட்ட கோணம்.

முக்கோணவியல் சார்புகளற்ற வாய்பாடுகள்

$K=\sqrt{(s-a)(s-b)(s-c)(s-d)-\frac{ac+bd+pq}{4}(ac+bd-pq)},$

இதில் நாற்கரத்தின் பக்கங்கள் வார்ப்புரு:Math, வார்ப்புரு:Math, வார்ப்புரு:Math, வார்ப்புரு:Math; அரைச்சுற்றளவு வார்ப்புரு:Math; மூலைவிட்டங்கள் வார்ப்புரு:Math, வார்ப்புரு:Math வட்ட நாற்கரத்தில் வார்ப்புரு:Math ஆக இருக்கும் என்பதால் இது பிரம்மகுப்தரின் வாய்பாடு ஆகச் சுருங்கும்.

$K=\frac{\sqrt{4p^2{q}^2-{(a^2+c^2-b^2-d^2)}^2}}{4}.$

இருநடுக்கோடுகள் வார்ப்புரு:Math, வார்ப்புரு:Math, மூலைவிட்டங்கள் வார்ப்புரு:Math, வார்ப்புரு:Math வாயிலாகப் பரப்பளவு:

$K=\frac{\sqrt{(m+n+p)(m+n-p)(m+n+q)(m+n-q)}}{2},$

$K=\frac{\sqrt{p^2{q}^2-(m^2-n^2{)}^2}}{2}.$ வார்ப்புரு:Rp

வார்ப்புரு:Math, வார்ப்புரு:Math, வார்ப்புரு:Math, வார்ப்புரு:Math நான்கும் $p^2+q^2=2(m^2+n^2)$எனத் தொடர்புடையவை. இவை நான்கில் எவையேனும் மூன்றின் அளவுகளை மட்டும்கொண்டும் பரப்பளவு காண முடியும்.வார்ப்புரு:Rp எனவே கீழுள்ள வாய்பாடுகள் கிடைக்கின்றன:

இருநடுக்கோடுகளின் நீளங்களும் ஒரு மூலைவிட்டமும் பயன்படுத்தி பரப்பளவின் வாய்பாடு:

$K=\frac{\sqrt{[(m+n{)}^2-p^2]\cdot [p^2-(m-n{)}^2]}}{2},$

இரு மூலைவிட்டங்களும் ஒரு இருநடுக்கோடும் கொண்ட வாய்பாடு:

$K=\frac{\sqrt{[(p+q{)}^2-4m^2]\cdot [4m^2-(p-q{)}^2]}}{4},$

திசையன் வாய்பாடுகள்

திசையன்களைப் பயன்படுத்தி நாற்கரம் வார்ப்புரு:Math இன் பரப்பளவின் வாய்பாடு:

$K=\frac{|𝐀𝐂\times 𝐁𝐃|}{2},$ (வார்ப்புரு:Math, வார்ப்புரு:Math திசையன்கள், நாற்கரத்தின் மூலைவிட்டங்கள்)

இது, வார்ப்புரு:Math, வார்ப்புரு:Math திசையன்களின் குறுக்குப் பெருக்கத்தின் மட்டு அளவில் பாதியாகும். இரு பரிமாண யூக்ளிடிய தளத்தில் இவ்விரு திசையன்களும் வார்ப்புரு:Math, வார்ப்புரு:Math எனில் பரப்பளவின் வாய்பாடு பின்வருமாறு அமையும்:

$K=\frac{|x_1{y}_2-x_2{y}_1|}{2}.$

மூலைவிட்டங்கள்

மூலைவிட்டங்களின் பண்புகள்

கீழுள்ள அட்டவணையில் சில அடிப்படையான நாற்கரங்களின் மூலைவிட்டங்கள் இருசமக்கூறிடுபவையா, செங்குத்தானவையா அல்லது சமமானவையான எனத் தரப்பட்டுள்ளது.

நாற்கரம்	இருசமக்கூறிடும் மூலைவிட்டங்கள்	செங்குத்து மூலைவிட்டங்கள்	சம மூலைவிட்டங்கள்
சரிவகம்	இல்லை		இல்லை
இருசமபக்க சரிவகம்	இல்லை		உண்டு
இணைகரம்	உண்டு	இல்லை	இல்லை
பட்டம்		உண்டு
செவ்வகம்	உண்டு	இல்லை	உண்டு
சாய்சதுரம்	உண்டு	உண்டு	இல்லை
சதுரம்	உண்டு	உண்டு	உண்டு

மூலைவிட்டங்களின் நீளங்கள்

ABCD நாற்கரத்தின் இரு பக்கங்கள், ஒரு மூலைவிட்டம் ஆகியவற்றால் அமையும் முக்கோணங்கள் ஒவ்வொன்றிலும் கோசைன் விதியைப் பயன்படுத்தி மூலைவிட்டங்களின் நீளங்களைக் காணலாம்:

$p=\sqrt{a^2+b^2-2ab\cos B}=\sqrt{c^2+d^2-2cd\cos D}$

$q=\sqrt{a^2+d^2-2ad\cos A}=\sqrt{b^2+c^2-2bc\cos C}.$

மேலும் சமச்சீர்மையுள்ள பிற வாய்பாடுகள்:

$p=\sqrt{\frac{(ac+bd)(ad+bc)-2abcd(\cos B+\cos D)}{ab+cd}}$

$q=\sqrt{\frac{(ab+cd)(ac+bd)-2abcd(\cos A+\cos C)}{ad+bc}}.$

இணைகரவிதியும், தொலெமியின் தேற்றத்தின் பொதுமைப்படுத்தலும்

எந்தவொரு குவிவு நாற்கரத்திலும் அதன் நான்கு பக்க நீளங்களின் வர்க்கங்ளின் கூட்டுத்தொகையானது, அதன் மூலைவிட்ட நீளங்களின் வர்க்கங்கள், மூலைவிட்டங்களின் நடுப்புள்ளிகளை இணைக்கும் கோட்டுத்துண்டின் நீளத்தின் வர்க்கத்தின் நான்கு மடங்கு இவற்றின் கூட்டுத்தொகைக்குச் சமமாக இருக்கும். அதாவது குவிவு நாற்கரம் ABCD எனில்:

$a^2+b^2+c^2+d^2=p^2+q^2+4x^2$ இதில், மூலைவிட்டங்களின் நடுப்புள்ளிகளை இணைக்கும் கோட்டுத்துண்டின் நீளம் x.வார்ப்புரு:Rp இம்முடிவானது ஆய்லரின் நாற்கரத் தேற்றம் என அறியப்படுவதோடு, இணைகர விதியின் பொதுமைப்படுத்தலுமாக உள்ளது.

1842 இல் செருமானியக் கணிதவியலாளர் கார்ல் ஆன்டன் பிரெட்ஷ்ணைடர், தொலெமியின் தேற்றத்தின் பொதுமைப்படுத்தலைக் கீழுள்ளவாறு தந்துள்ளார். இது குவிவு நாற்கரத்தின் இரு மூலைவிட்ட நீளங்களின் வர்க்கங்களின் பெருக்குத்தொகையினைத் தருகிறது:

$p^2{q}^2=a^2{c}^2+b^2{d}^2-2abcd\cos (A+C).$

இதனை நாற்கரங்களுக்கான கோசைன் விதியாகக் கொள்ளலாம். வட்ட நாற்கரத்தில் A + C = 180° என்பதால் cos (A + C) = −1. எனவே இம்முடிவு pq = ac + bd எனச் சுருங்கும்.

கோண இருசமவெட்டிகள்

ஒரு குவிவு நாற்கரத்தின் உட்கோண இருசமவெட்டிகள் ஒரு வட்ட நாற்கரத்தை அமைக்கும்வார்ப்புரு:Rp (அதாவது அடுத்துள்ள கோணங்களின் இருசமவெட்டிகள் சந்திக்கும் புள்ளிகள் ஒரே வட்டத்தின் மீதமையும்) அல்லது, நான்கு உட்கோண இருசமவெட்டிகளும் ஒரே புள்ளியில் சந்திக்கும். பிந்தைய வகையில் நாற்கரமானது, தொடு நாற்கரமாக இருக்கும்.

ABCD நாற்கரத்தின் A, C கோணங்களின் இருசமவெட்டிகள் சந்திக்கும் புள்ளி மூலைவிட்டம் BD இன் மீதமைந்தால். B, D கோணங்களின் இருசமவெட்டிகள் மூலைவிட்டம் AC இன் மீது அமையும்.

இருநடுக்கோடுகள்

நாற்கரத்தின் பக்க நடுப்புள்ளிகளை இணைக்கும் இணைகரம் EFGH

ஒரு நாற்கரத்தின் எதிர்ப்பக்கங்களின் நடுப்புள்ளிகளை இணைக்கும் கோட்டுத்துண்டுகள் இருநடுக்கோடுகள் எனப்படும். இரு நடுக்கோடுகள் வெட்டும்புள்ளி நாற்கரத்தின் உச்சிகளின் திணிவு மையம் ஆகும்.

எந்தவொரு நாற்கரத்தின் (குவிந்த, குழிந்த, குறுக்கு நாற்கரங்கள்) பக்கங்களின் நடுப்புள்ளிகள் ஒரு இணைகரத்தின் உச்சிப் புள்ளிகளாகும்.

இந்த இணைகரத்தின் பண்புகள்:

• இணைகரத்தின் ஒவ்வொரு சோடி எதிர்ப்பக்கங்களும் மூல நாற்கரத்தின் மூலைவிட்டத்திற்கு இணையாகும்.
• இணைகரத்தின் ஒரு பக்கத்தின் நீளம் அப்பக்கம் எந்த மூலைவிட்டத்திற்கு இணையாக இருக்கிறதோ அதன் நீளத்தில் பாதி.
• இணைகரத்தின் பரப்பளவு, மூல நாற்கரத்தின் பரப்பளவில் பாதி.
• இணைகரத்தின் சுற்றளவு, மூல நாற்கரத்தின் மூலைவிட்டங்களின் கூட்டுத்தொகைக்குச் சமமாக இருக்கும்.
• இணைகரத்தின் மூலைவிட்டங்கள் மூல முக்கோணத்தின் இருநடுக்கோடுகளாக இருக்கும்.

மூல நாற்கரத்தின் இரண்டு இருநடுக்கோடுகளும் மூலைவிட்டங்களின் நடுப்புள்ளிகளை இணைக்கும் கோட்டுத்துண்டும் ஒரே புள்ளியில் சந்திக்கும் கோடுகளாக இருக்கும். மேலும் அவை சந்திக்கும் புள்ளி அவற்றை இருசமக்கூறிடும்.வார்ப்புரு:Rp

ஒரு குவிவு நாற்கரத்தின் பக்கங்கள் a, b, c, d எனில், a, c பக்கங்களின் நடுப்புள்ளிகளை இணைக்கும் இருநடுக்கோட்டின் நீளம்:

$m=\frac{1}{2}\sqrt{-a^2+b^2-c^2+d^2+p^2+q^2}$ (p, q மூலைவிட்ட நீளங்கள்)

b, d பக்கங்களின் நடுப்புள்ளிகளை இணைக்கும் இருநடுக்கோட்டின் நீளம்:

$n=\frac{1}{2}\sqrt{a^2-b^2+c^2-d^2+p^2+q^2}.$

இவ்விரு முடிவுகளிலிருந்து பின்வரும் மதிப்பைப் பெறலாம்.

$p^2+q^2=2(m^2+n^2).$வார்ப்புரு:Rp

இருநடுக்கோடுகளின் நீளங்களை எதிர்ப்பக்க நீளங்கள், மூலைவிட்டங்களின் நடுப்புள்ளிகளுக்கு இடைப்பட்ட தூரம் ஆகியவற்றின் வாயிலாக எழுதலாம். ஆய்லரின் நாற்கரத் தேற்றத்தைப் பயன்படுத்தி இதனைப் பெறலாம்:

$m=\frac{1}{2}\sqrt{2(b^2+d^2)-4x^2}$

$n=\frac{1}{2}\sqrt{2(a^2+c^2)-4x^2}.$

ஒவ்வொரு இருநடுக்கோட்டு நீள வாய்பாட்டிலும் உள்ள எதிர்ப்பக்கங்கள், அந்த இருநடுக்கோடுகள் இணைக்கும் எதிர்ப்பக்கங்கள் இல்லை.

குவிவு நாற்கரத்தில், இருநடுக்கோடுகளுக்கும் மூலைவிட்டங்களுக்குமிடையே பின்வரும் இரும இணைப்பு இருப்பதைக் காணலாம்:

• இரு மூலைவிட்டங்களும் செங்குத்தாக இருந்தால், இருந்தால் மட்டுமே, இருநடுக்கோடுகள் இரண்டும் சமநீளமுள்ளவை.
• இரு மூலைவிட்டங்களும் சமநீளமுள்ளவையாக இருந்தால், இருந்தால் மட்டுமே, இருநடுக்கோடுகள் இரண்டும் செங்குத்தானவை.

முக்கோணவியல் முற்றொருமைகள்

நாற்கரம் ABCD இன் நான்கு கோணங்களும் பின்வரும் முற்றொருமைகளை நிறைவு செய்யும்:

$\sin A+\sin B+\sin C+\sin D=4\sin \frac{A+B}{2}\sin \frac{A+C}{2}\sin \frac{A+D}{2}$

$\frac{\tan A\tan B-\tan C\tan D}{\tan A\tan C-\tan B\tan D}=\frac{\tan (A+C)}{\tan (A+B)}.$

$\frac{\tan A+\tan B+\tan C+\tan D}{\cot A+\cot B+\cot C+\cot D}=\tan A\tan B\tan C\tan D.$

tan 90° இன் மதிப்பு வரையறுக்கப் படாததால், கடைசி இரு முற்றொருமைகளிலும் எந்தவொரு கோணமும் செங்கோணமாக இருக்க முடியாது.

$a$, $b$, $c$, $d$ குவிவு நாற்கரத்தின் பக்கங்கள்; $s$ அரைச்சுற்றளவு; $A,$ $C$ எதிர்கோணங்கள் எனில்:

$ad{\sin }^2\frac{A}{2}+bc{\cos }^2\frac{C}{2}=(s-a)(s-d)$

$bc{\sin }^2\frac{C}{2}+ad{\cos }^2\frac{A}{2}=(s-b)(s-c)$.

இவற்றைப் பயன்படுத்தி பிரெட்ஷ்ணைடரின் வாய்பாட்டைப் பெறலாம்.

சமனிலிகள்

பரப்பளவு

குவிவு நாற்கரத்தின் பக்க நீளங்கள் a, b, c, d; மூலைவிட்டங்கள் p, q எனில் பரப்பளவு K நிறைவு செய்யும் சமனிலிகள்:

$K\le \frac{1}{4}(a+c)(b+d)$ செவ்வகத்துக்கு மட்டுமே சமக்குறி பொருந்தும்.

$K\le \frac{1}{4}(a^2+b^2+c^2+d^2)$ சதுரத்துக்கு மட்டுமே சமக்குறி பொருந்தும்.

$K\le \frac{1}{4}(p^2+q^2)$ மூலைவிட்டங்கள் செங்குத்தாக இருந்தால் மட்டுமே சமக்குறி பொருந்தும்.

$K\le \frac{1}{2}\sqrt{(a^2+c^2)(b^2+d^2)}$ செவ்வகத்துக்கு மட்டுமே சமக்குறி பொருந்தும்.

பிரெட்ஷ்ணைடரின் வாய்பாடு மூலம் நாற்கரத்தின் பரப்பளவு:

$K\le \sqrt{(s-a)(s-b)(s-c)(s-d)}$ வட்ட நாற்கரமாக இருந்தால், இருந்தால் மட்டுமே, சமக்குறி பொருந்தும்.

பரப்பளவு நிறைவு செய்யும் மற்றொரு சமனிலி:

$K\le \frac{1}{2}\sqrt[3]{(ab+cd)(ac+bd)(ad+bc)}.$

நாற்கரத்தின் சுற்றளவு L எனில்வார்ப்புரு:Rp

$K\le \frac{1}{16}{L}^2,$ சமக்குறி சதுரத்துக்கு மட்டுமே பொருந்தும்.

p, q மூலைவிட்டங்கள் எனில்:

$K\le \frac{1}{2}pq$, மூலைவிட்டங்கள் செங்குத்தாக இருந்தால் மட்டுமே சமக்குறி பொருந்தும்.

$K\le \frac{a^2+b^2+c^2+d^2+p^2+q^2+pq-ac-bd}{8}$ சதுரத்துக்கு மட்டுமே சமக்குறி பொருந்தும்.

$K\le \frac{1}{3+\sqrt{3}}(ab+ac+ad+bc+bd+cd)-\frac{1}{2(1+\sqrt{3}{)}^2}(a^2+b^2+c^2+d^2)$ சதுரத்துக்கு மட்டுமே சமக்குறி பொருந்தும்.

மூலைவிட்டங்கள், இருநடுக்கோடுகள்

ஆய்லரின் நாற்கரத் தேற்றத்தின் கிளைமுடிவுச் சமனிலி:

$a^2+b^2+c^2+d^2\ge p^2+q^2,$ இணைகரத்துக்கு மட்டுமே சமக்குறி பொருந்தும்.

வட்ட நாற்கரத்துக்குச் சமனியாகவுள்ள தொலெமியின் தேற்ற முடிவைப் பொதுமைப்படுத்தி குவிவு நாற்கரத்துக்கு சமனிலியாக ஆய்லர் மாற்றியுள்ளார்:

$pq\le ac+bd$வார்ப்புரு:Rp பெரும்பாலும் இது தொலெமியின் சமனிலி எனப்படுகிறது.

இருநடுக்கோடுகள் m, n; மூலைவிட்டங்கள் p, q எனில் அவற்றைத் தொடர்புபடுத்தும் சமனிலி:

$pq\le m^2+n^2,$ மூலைவிட்டங்கள் சமமாக இருந்தால் மட்டுமே, சமக்குறி பொருந்தும்.வார்ப்புரு:Rp $m^2+n^2=\frac{1}{2}(p^2+q^2).$ முற்றொருமையிலிருந்து இச்சமனிலி நேரிடையாகப் பெறப்படுகிறது.

பக்கங்கள்

நாற்கரத்தின் பக்கங்கள் a, b, c, d நிறைவுசெய்யும் சமனிலிகள்:

$a^2+b^2+c^2>\frac{d^2}{3}$வார்ப்புரு:Rp

$a^4+b^4+c^4\ge \frac{d^4}{27}.$வார்ப்புரு:Rp

பெரும, சிறுமப் பண்புகள்

குறிப்பிட்ட சுற்றளவுள்ள எல்லா நாற்கரங்களிலும் மிக அதிகப் பரப்பளவுள்ள நாற்கரம் ஒரு சதுரமாக இருக்கும். இதனைக் கீழுள்ள சமனிலியிலிருந்து பெறலாம்.வார்ப்புரு:Rp

$K\le \frac{1}{16}{L}^2$, K - பரப்பளவு; L சுற்றளவு. நாற்கரம், சதுரமாக இருந்தால், இருந்தால் மட்டுமே, சமக்குறி பொருந்தும். இதேபோல ஒரே பரப்பளவுள்ள நாற்கரங்களில் மிகச் சிறியளவு சுற்றளவுள்ளது சதுரம்.

தரப்பட்ட பக்கநீளங்கள் கொண்ட நாற்கரங்களில் அதிகபட்ச பரப்பளவு கொண்டது வட்ட நாற்கரம்.

தரப்பட்ட மூலைவிட்டங்களையுடைய குவிவு நாற்கரங்களில் மிக அதிகப் பரப்பளவு கொண்டது செங்குத்து மூலைவிட்ட நாற்கரம்.வார்ப்புரு:Rp இதனை நேரிடையாகக் பின்வரும் பரப்பளவு சமனிலியிலிருந்து பெறலாம்:

$K=\frac{1}{2}pq\sin \theta \le \frac{1}{2}pq,$ மூலைவிட்டங்கள் p, q க்கு இடைப்பட்ட கோணம் θ. θ = 90° ஆக இருந்தால், இருந்தால் மட்டுமே, சமக்குறி பொருந்தும்.

குவிவு நாற்கரம் ABCD இன் உள்ளமையும் புள்ளி P எனில்::$AP+BP+CP+DP\ge AC+BD.$

இச்சமனிலியிலிருந்து, நாற்கரத்தின் உச்சிகளிலிருந்துள்ள தூரங்களின் கூட்டுத்தொகையை சிறுமமாகக் கொண்ட உள்ளமை புள்ளி மூலைவிட்டங்கள் வெட்டிக்கொள்ளும் புள்ளி என அறியலாம். எனவே இப்புள்ளி குவிவு நாற்கரத்தின் பெர்மா புள்ளியாகும்வார்ப்புரு:Rp

குவிவு நாற்கரங்களின் பிற பண்புகள்

• நாற்கரத்தி எல்லாப் பக்கங்களின் மீதும் வெளிப்புறமாக சதுரங்கள் வரையப்பட்டால், எதிரெதிர் சதுரங்களின் மையங்களை இணைக்கும் கோட்டுத்துண்டுகள் சம நீளமுள்ளவை; செங்த்தானவை. இவை ஒரு செங்குத்து மூலைவிட்ட நாற்கரத்தின் உச்சிகளாக இருக்கும்.
• ஒரு எளிய நாற்கரத்தின் பக்கங்களுக்கு சமமான பக்கங்களைக் கொண்ட ஒரு வட்ட நாற்கரம் இருக்கும்.
• நாற்கரத்தின் மூலைவிட்டங்கள், பக்கங்களால் உருவாகும் நான்கு முக்கோணங்களில், ஒரு சோடி எதிர் முக்கோணங்களின் பரப்பளவுகளின் பெருக்குத்தொகை மற்ற இரு முக்கோணங்களின் பரப்பளவுகளின் பெருக்குத்தொகைக்குச் சமமாக இருக்கும்.

வெளியிணைப்புகள்

• வார்ப்புரு:Springer
• Quadrilaterals Formed by Perpendicular Bisectors, Projective Collinearity and Interactive Classification of Quadrilaterals from cut-the-knot
• Definitions and examples of quadrilaterals and Definition and properties of tetragons from Mathopenref
• A (dynamic) Hierarchical Quadrilateral Tree at Dynamic Geometry Sketches
• An extended classification of quadrilaterals வார்ப்புரு:Webarchive at Dynamic Math Learning Homepage வார்ப்புரு:Webarchive
• The role and function of a hierarchical classification of quadrilaterals by Michael de Villiers