அப்பொலோனியசின் கணக்கு

படம் 2: தரப்பட்ட கருப்பு வண்ண மூன்று வட்டங்களின் தொடுவட்டங்களாக அமையும் நான்கு இணைச்சோடி தீர்வுகள்.

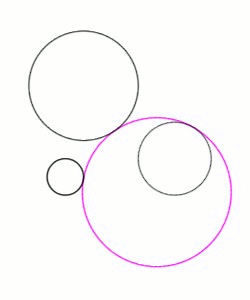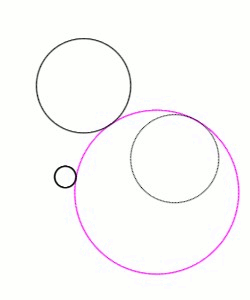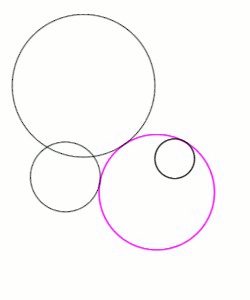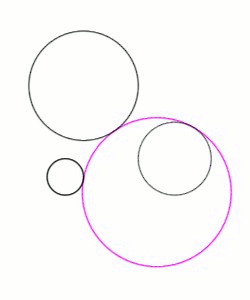
யூக்ளிடிய தள வடிவவியலில் அப்பொலோனியசின் கணக்கு (Problem of Apollonius) என்பது ஒரு தளத்தில் அமைந்த மூன்று வட்டங்களுக்கு தொடுவட்டங்களாக அமையும் வட்டங்களை வரைதலாகும்.(படம் 1). இக்கணக்கு பெர்காவின் கணிதவியலாளர் அப்பொலோனியசால் (கிமு 262 - கிமு 190) முன்வைக்கப்பட்டு தீர்வும் காணப்பட்டது. இக்கணக்கையும் அதன் தீர்வையும் கொண்ட அவரது படைப்பான எபாஃபாய் (வார்ப்புரு:Lang- வார்ப்புரு:Lang, "Tangencies-தொடுநிலைகள்") காலப்போக்கில் மறைந்து போனாலும் 4 ஆம் நூற்றாண்டில் அலெக்சாந்திரியாவின் பாப்பஸ் எனும் கணிதவியலாளரின் குறிப்புகளால் மீட்டெடுக்கப்பட்டது. தரப்பட்ட மூன்று வட்டங்களையும் தொடும் வட்டங்கள் மொத்தம் 8 உள்ளன (படம் 2).

ரெனே டேக்கார்ட், தரப்பட்ட மூன்று வட்டங்கள் மற்றும் அவை மூன்றையும் தொடும் வட்டம் ஆகியவற்றின் ஆரங்களுக்கு இடையேயுள்ள தொடர்பை டேக்கார்ட்டின் தேற்றம் வாயிலாகத் தந்துள்ளார். அப்பொலோனியசின் இக்கணக்கு முப்பரிமாணத்திற்குப் பொதுமைப்படுத்தப்பட்டுள்ளது: அது தரப்பட்டுள்ள மூன்று கோளங்களைத் தொட்டவாறு அமையும் நான்காவது கோளம் காண்பதாகும்.

கூற்று

அப்பொலோனியசின் கணக்கின் பொதுக்கூற்று

ஒரு தளத்தில் அமையும் மூன்று வடிவவியல் பொருட்களைத் தொடுகின்ற ஒன்று அல்லது ஒன்றுக்கும் மேற்பட்ட வட்டங்களை வரைதலாகும். எடுத்துக்கொள்ளப்படும் மூன்று வடிவவியல் பொருட்கள் புள்ளிகளாகவோ, கோடுகளாகவோ அல்லது வட்டங்களாகவோ இருக்கலாம்.^[1]^[2]^[3]^[4] இம்மூன்றும் எவ்விதத்திலும் அமையலாம்; ஒன்றையொன்று குறுக்கிடலாம்; ஆனால் அவை மூன்றும் வெவ்வேறானவையாக இருத்தல் அவசியம்; அதாவது அவை ஒன்றோடொன்று பொருந்துதல் கூடாது.

தொடுநிலையின் வரையறை:

ஒரு புள்ளி, ஒரு கோடு, ஒரு வட்டம் ஆகிய மூன்றும் தனக்குத்தானே தொடுநிலையில் அமையும். எனவே ஒரு வட்டமானது ஏதேனும் இரு வட்டங்களைத் தொட்டவாறு இருக்குமானால் அதையும் சேர்த்து அது மூன்று வட்டங்களைத் தொடுவதாகக் கணக்கில்கொண்டு, அவ்வட்டத்தை அப்பலோனியஸ் கணக்கின் தீர்வாகக் கொள்ளலாம்.

இரு வடிவவியல் பொருட்களுக்கிடையே ஒரு பொதுப்புள்ளி இருக்குமானால் அவை இரண்டும் ஒன்றையொன்று வெட்டுவதாகக் கொள்ளப்படும். எனவே வரையறைப்படி, ஒரு கோடு அல்லது வட்டத்தின் மீது ஒரு புள்ளி அமையுமானல் அப்புள்ளி, அக்கோட்டிற்கோ அல்லது வட்டத்துக்கு தொடுநிலையில் அமையும்; என்வே வெவ்வேறான இரு புள்ளிகள் தொடுநிலையில் இராது.

இரு வெவ்வேறான கோடுகளோ அல்லது வட்டங்களோ வெட்டிக் கொள்ளும் புள்ளியில் ஏற்படும் கோணம் பூச்சியமாக இருந்தால் அவை தொடுநிலையில் உள்ளன எனப்படும். அந்நிலையில் அவை வெட்டிக்கொள்ளும் புள்ளி தொடுபுள்ளி எனப்படும். இது ஒரு கோடு, ஒரு வட்டம் ஆகிய இரண்டுக்கும் பொருந்தும். இரு இணைகோடுகளை ஒன்றுக்கொன்று முடிவிலியில் தொடும் கோடுகளாகக் கருத முடிந்தாலும் பொதுவாக வெவ்வேறான இரு கோடுகள் ஒன்றுக்கொன்று தொடுகோடுகளாக இருக்க முடியாது.^[5]^[6] தீர்வு வட்டம் தரப்பட்ட மூன்று வட்டங்களையும் உட்புறமாகவோ அல்லது வெளிப்புறமாகவோ தொடலாம்.

தரப்பட்ட மூன்று புள்ளிகளில் இருந்து உள்ள தூரங்களின் வித்தியாசம், மதிப்பறியப்பட்டவையாக உள்ளபடி அமையும் ஒன்று அல்லது ஒன்றுக்கும் மேற்பட்ட புள்ளிகளைக் காண்பதாகவும் அப்பலோனியசின் கணக்கின் கூற்றைக் கூறலாம்:

தரப்பட்ட வட்டங்களின் ஆரங்கள் r₁, r₂ and r₃; தீர்வு வட்டத்தின் ஆரம் r_s எனில் தீர்வு வட்டம் தரப்பட்ட வட்டங்களை வெளிப்புறமாகத் தொடும்போது அதன் மையத்திற்கும் மற்ற மூன்று வட்டங்களின் மையங்களுக்கும் இடைப்பட்ட தொலைவுகள் முறையே:

d_{1} = r_{1} + r_{s}

d_{2} = r_{2} + r_{s}

d_{3} = r_{3} + r_{s}

மேலும் இத்தொலைவுகளுக்கிடையுள்ள வித்தியாசங்கள் மாறிலிகளாக இருக்கின்றன. அவை தெரிந்த ஆரங்களின் மதிப்புகளின் வாயிலாக அமைகின்றன:

d_{1} - d_{2} = r_{1} - r_{2}

d_{2} - d_{3} = r_{2} - r_{3}

d_{3} - d_{1} = r_{3} - r_{1}

இதனைத் தரப்பட்ட வட்டங்களைத் தீர்வு வட்டமானது உட்புறமாகத் தொடும்போதும் காணலாம்.

வரலாறு

வடிவவியல் கணக்குகளிலேயே பிரபலமானதாகக் கருதப்பட்ட^[3] அப்பலோனியசின் கணக்கிற்கு வடிவவியல் மற்றும் இயற்கணித தீர்வுகள் கண்டுபிடிக்கப்பட்டன. அப்பலோனியசின் கணக்கு மற்றும் தீர்வும் காலப்போக்கில் மறைந்து போனாலும் அலெக்சாந்திரியாவின் பாப்பசின் குறிப்புகளைக் கொண்டு பிரெஞ்சு கணிதவியலாளர் ஃபிரான்சுவா வியேட் மற்றும் பலரால் அவை மீளமைக்கப்பட்டன.^[7]^[8] இக்கணக்கிற்கான முதலாவது புதுத்தீர்வு 1596 ஆம் ஆண்டு ஏட்ரியான் வோன் ரூமெனால் வெளியிடப்பட்டது. இவர் தீர்வு வட்டங்களின் மையங்களை இரு அதிபரவளையங்களின் வெட்டும் புள்ளிகளாக அமைவதைக் கண்டறிந்தார்.^[9]^[10] வோன் ரூமெனின் தீர்வுமுறை 1687 இல் நியூட்டனாலும்,^[11]^[12] பின்னர் 1881 இல் கணிதவியலாளர் ஜான் கேசியாலும் சீரமைக்கப்பட்டது.^[13]

வான் ரூமனின் தீர்வுமுறையில் அப்பலோனியசின் கணக்கின் தீர்வினைக் கவராயம் மற்றும் நேர்விளிம்பு மட்டும் பயன்படுத்திக் கண்டுபிடிக்க முடியவில்லை. அப்பலோனியசின் கணக்கிற்குத் தீர்வுகாண வோன் ரூமெனை ஊக்கப்படுத்திய அவரது நண்பர் ஃபிரான்சுவா வியேட் அத்தீர்வினைக் கவராயம் மற்றும் நேர்விளிம்பு மட்டும் பயன்படுத்திக் கண்டுபிடித்தார்.^[14] இவரது தீர்வுமுறை அப்பலோனியசின் தீர்வோடு அதிகம் பொருந்தியது. பிற தீர்வுகள், மூன்று வெவ்வேறு கணிதவியலாளர்களால் வெளியிடப்பட்டது.^[15]

மேலும் பல வடிவவியல் தீர்வுகள் 19 ஆம் நூற்றாண்டில் கண்டறியப்பட்டன. அவற்றுள் ழான் விக்டர் போன்செலாட்டின் (1811) தீர்வும்^[16], ஜோசப் டியாஸ் கொர்கோனின் (1814) தீர்வும் குறிப்பிடத்தக்கன.^[17]

17 ஆம் நூற்றாண்டின் ரெனே டேக்கார்ட் மற்றும் பொகிமியாவின் இளவரசி எலிசபெத் இருவரும் இக்கணக்கின் இயற்கணித தீர்வுகளின் முன்னோடிகள் ஆவர். இவர்களது தீர்வுகள் சற்று சிக்கலானவையாக இருந்தன^[18]^[19]. பின்னர் 18 மற்றும் 19 ஆம் நூற்றாண்டுகளில் இக்கணக்கிற்கு இயற்கணித முறையில் தீர்வு கண்டவர்கள் லியோனார்டு ஆயிலர்^[20], நிக்கோலஸ் ஃபஸ்,^[18] கார்ல் ஃப்ரெடெரிக் காஸ்,^[21] லசார் கார்னோ^[22] அகஸ்டின் லூயிஸ் கோஷி^[23] ஆவர்.

தீர்வு முறைகள்

ஏட்ரியான் வோன் ரூமெனின் (1596) தீர்வு முறை

ஏட்ரியான் வோன் ரூமெனின் (1596) தீர்வு முறை இரு வெட்டிக்கொள்ளும் அதிபரவளைவுகளை அடிப்படையாகக் கொண்டிருந்தது.^[9]^[10] எடுத்துக்கொள்ளப்பட்ட மூன்று வட்டங்கள் C₁, C₂ and C₃. வோன் ரூமென் முதலில் இரண்டு வட்டங்களைத் தொடுகின்ற வட்டத்தைக் கண்டுபிடித்தார். எடுத்துக்கொள்ளப்பட்ட இரண்டு வட்டங்களின் மையங்களைக் குவியங்களாகக் கொண்டு வரையப்பட்ட அதிபரவளைவின் மீது அவ்விரு வட்டங்களையும் தொடும் வட்டத்தின் மையம் அமைவதைக் கண்டறிந்தார். எடுத்துக்கொள்ளப்பட்ட இரு வட்டங்கள் C₁, C₂; அவற்றின் ஆரங்கள் r₁ and r₂; தொடும் வட்டத்தின் ஆரம் r_s (படம் 3). தீர்வு வட்டத்தின் மையத்திற்கும் C₁ வட்ட மையத்திற்கும் இடையேயுள்ளதூரம் d₁, வெளிப்புறமாகத் தொடும்போது வார்ப்புரு:Nowrap ஆகவும் உட்புறமாகத் தொடும்போது வார்ப்புரு:Nowrap ஆகவும் இருக்கும். இதேபோல் தீர்வு வட்டத்தின் மையத்திற்கும் C₂ வட்ட மையத்திற்கும் இடையேயுள்ளதூரம் d₂, வெளிப்புறமாகத் தொடும்போது வார்ப்புரு:Nowrap ஆகவும் உட்புறமாகத் தொடும்போது வார்ப்புரு:Nowrap ஆகவும் இருக்கும். இவ்விரு தொலைவுகளின் வித்தியாசம் வார்ப்புரு:Nowrap எப்பொழுதும் ஒரு மாறிலியாகவே இருக்கும். எனவே தீர்வுவட்ட மையம் மற்ற இரு வட்ட மையங்களைக் குவியங்களாகக் கொண்ட அதிபரவளைவின் மீது அமையும். இதேபோல C₂, C₃ வட்டங்களை எடுத்துக்கொண்டு தீர்வுவட்ட மையம் அமையும் மற்றொரு அதிபரவளையத்தையும் காணலாம். ஆனால் தீர்வு வட்டமும் C₂ வட்டமும் இரண்டு நிலைகளிலும் தொட்டுக்கொள்ளும் விதங்கள் (வெளிப்புறமாக அல்லது உட்புறமாக) ஒத்துப்போகுமாறு பார்த்துக்கொள்ள வேண்டும். இவ்விரு அதிபரவளைவுகளும் வெட்டும் புள்ளியே தீர்வு வட்டத்தின் மையம். தீர்வு வட்டம் மூன்று வட்டங்களைத் தொடும்விதங்களின் மாற்றத்தால் வெவ்வேறு தீர்வு வட்டங்களைக் காணலாம்.

ஃபிரான்சுவா வியேட்டின் தீர்வு

கீழேதரப்பட்டுள்ளபடி அப்பொலொனியசின் கணக்கிற்கு பத்து சிறப்புவகைகள் உள்ளன. இவ்வகைகள், எடுத்துக்கொள்ளப்படும் மூன்று வடிவவியல் பொருள்களின் தன்மையைப் பொறுத்து அமைகின்றன. மூன்று பொருட்கள், வட்டம் (C), கோடு (L), புள்ளி (P) ஆகிய ஏதாவது ஒன்றாக அமையலாம். அவற்றின் அமைவுகளைப் பொறுத்து பத்து சிறப்புவகைகளும் குறிக்கப்படுகிறது. எடுத்துக்காட்டாக, மூன்று வடிவவியல் பொருட்களில் இரண்டு வட்டமாகவும் ஒன்று புள்ளியாகவும் இருப்பின் அவ்வகையின் குறியீடு CCP.^[24] வியேட் பத்து வகைகளுக்கும் கவராயமும் நேர்விளிம்பும் மட்டுமே கொண்டு காணக்கூடிய தீர்வுகளைக் கண்டறிந்தார். எளிதான வகைகளின் தீர்வுகளை முதலில் கண்டு, பின்னர் அதனைப் பயன்படுத்தி சிக்கலான வகைகளின் தீர்வுகளைக் கண்டார்.^[1]^[14]

Figure 4: Tangency between circles is preserved if their radii are changed by equal amounts. A pink solution circle must shrink or swell with an internally tangent circle (black circle on the right), while externally tangent circles (two black circles on left) do the opposite.

வியேட் முதலில் PPP வகைக்குத் தீர்வு காண (மூன்று புள்ளிகள்) யூக்ளிடின் படைப்பான எலிமெண்ட்சிலுள்ள முறையைக் கையாண்டார். அத்தீர்விலிருந்து ஒரு புள்ளியின் படி தேற்றத்துக்கு ஒத்ததாக ஒரு முற்கோளை (lemma) உருவாக்கி அதன் மூலம் LPP வகைக்குத் தீர்வு கண்டார். மீண்டும் யூக்ளிடைப் பின்பற்றி கோண இருசமவெட்டிகளைப் பயன்படுத்தி LLL வகைக்குத் தீர்வு கண்டார். பின்னர் ஒரு புள்ளி வழியேச் செல்லும் கோண இருசமவெட்டிக்குச் செங்குத்துக் கோடு வரையும் முறைகாண ஒரு முற்கோளை உருவாக்கினார். அதனைப் பயன்படுத்தி LLP வகைக்குத் தீர்வு கண்டுபிடித்தார். இந்நான்கு வகைகளும் வட்டங்களில்லாமல் அமைந்த முதல் நான்கு வகைகளாகும்.

மீதமுள்ள வகைகளைத் தீர்ப்பதற்கு தரப்பட்ட வட்டங்களையும் அவற்றின் தீர்வு வட்டங்களையும் தொடுநிலைவிதம் மாறாமல் அளவு மாற்றும் முறையைப் பயன்படுத்தினார். (படம் 4). தீர்வு வட்டத்தின் ஆரம் Δr அளவு மாற்றப்பட்டால், தரப்பட்ட வட்டங்களில் உட்புறமாகத் தொடும் வட்டங்களின் ஆரம் Δr அளவும், வெளிப்புறமாகத் தொடும் வட்டங்களின் ஆரம் −Δr அளவும் மாற்றப்பட வேண்டும். அதாவது தீர்வு வட்டம் பெரிதாகும் போது தொடுநிலை மாறாமல் இருப்பதற்காகத் தரப்பட்ட வட்டங்களில், உட்தொடு வட்டங்கள் விரியும்; வெளித்தொடு வட்டங்கள் சுருங்கும்.

மீதமுள்ள ஆறு வகைககள்:

CLL வகையில் மூன்று வட்டங்களில் ஒன்று ஒரு புள்ளியாகச் சுருக்கி LLP வகையாக மாற்றியும்;
CLP வகை மூன்று முற்கோள்களைப் பயன்படுத்தியும்;
CCL வகையில் ஒரு வட்டத்தைப் புள்ளியாகச் சுருக்கி CLP வகைக்கு மாற்றியும்;
CPP வகையும்;
இரண்டு முற்கோள்களைப் பயன்படுத்தி CCP வகையும்;
இறுதியாக CCC வகையில் ஒரு வட்டத்தைப் புள்ளியாகச் சுருக்கி CCP வகையாக மாற்றியும்

தீர்க்கப்பட்டன.

பத்து வகைகளின் பட்டியல்

அப்பொலோனியசின் கணக்கின் பத்து சிறப்பு வகைகள்
வரிசை எண்	குறியீடு	தரப்பட்ட வடிவவியல் பொருட்கள்	தீர்வுகளின் எண்ணிக்கை (பொதுவாக)
1	PPP	மூன்று புள்ளிகள்	1
2	LPP	ஒரு கோடு, இரு புள்ளிகள்	2
3	LLP	இரு கோடுகள், ஒரு புள்ளி	2
4	CPP	ஒரு வட்டம், இரு புள்ளிகள்	2
5	LLL	மூன்று கோடுகள்	4
6	CLP	ஒரு வட்டம், ஒரு கோடு, ஒரு புள்ளி	4
7	CCP	இரு வட்டங்கள், ஒரு புள்ளி	4
8	CLL	ஒரு வட்டம், இரு கோடுகள்	8
9	CCL	இரு வட்டங்கள், ஒரு கோடு	8
10	CCC	மூன்று வட்டங்கள்	8

இயற்கணித தீர்வுகள்

தீர்வு வட்டத்தின் ஆரம் மற்றும் மையங்களைக் காண உதவும் மூன்று சமன்பாடுகளின் தொகுதியாக அப்பொலோனியசின் கணக்கினை அமைக்கலாம்.^[25] எடுத்துக்கொள்ளப்படும் மூன்று வட்டங்களும் அவற்றின் தீர்வு வட்டமும் ஒரே தளத்தில் அமைவன என்பதால் கார்ட்டீசியன் ஆள்கூற்று முறைமைப்படி அவற்றின் அச்சுதூரங்களை முறையே (x₁, y₁), (x₂, y₂) and (x₃, y₃), (x_s, y_s) எனவும் அவற்றின் ஆரங்களை முறையே r₁, r₂, r₃, r_s எனவும் கொள்ளலாம். தீர்வு வட்டமானது தரப்பட்ட மூன்று வட்டங்களையும் தொடுவதற்கான நிலையை பின்வரும் சமன்பாட்டுத் தொகுதி தருகிறது:

{(x_{s} - x_{1})}^{2} + {(y_{s} - y_{1})}^{2} = {(r_{s} - s_{1} r_{1})}^{2}

{(x_{s} - x_{2})}^{2} + {(y_{s} - y_{2})}^{2} = {(r_{s} - s_{2} r_{2})}^{2}

{(x_{s} - x_{3})}^{2} + {(y_{s} - y_{3})}^{2} = {(r_{s} - s_{3} r_{3})}^{2} .

சமன்பாடுகளின் வலதுபுறமுள்ள s₁, s₂ and s₃ இன் மதிப்புகள் ±1 ஆக அமைகின்றன. தீர்வு வட்டம் தரப்பட்ட வட்டங்களில் ஒன்றை உட்புறமாகத் தொடும்போது s = 1 ஆகவும், வெளிப்புறமாகத் தொடும்போது s = −1 ஆகவும் இருக்கும். படம் 1 மற்றும் 4 இல் பிங்க் நிற தீர்வு வட்டம், வலப்புறமுள்ள நடுத்தர அளவு வட்டத்தை உட்புறமாகவும், இடதுபுறமுள்ள சிறிய மற்றும் பெரிய வட்டங்களை வெளிப்புறமாகவும் தொடுகிறது. தரப்பட்ட வட்டங்களை அவற்றின் ஆர அளவுகளைக் கொண்டு வரிசைப்படுத்தினால் இத்தீர்வுக்குரிய குறிகள் வார்ப்புரு:Nowrap. இம்மூன்று குறிகளையும் சார்பின்றி தேர்வு செய்யலாம் என்பதால் மொத்தம் வார்ப்புரு:Nowrap சமன்பாட்டுத் தொகுதிகள் கிடைக்கின்றன. ஒவ்வொரு தொகுதியும் அப்பொலோனியசின் கணக்கிற்கு ஒரு தீர்வினைத் தருவதால் மொத்தம் கிடைக்கக்கூடிய தீர்வுகள் எட்டாகும்.

மூன்று சமன்பாடுகளையும் விரித்து சுருக்கக் கிடைக்கும் மூன்று சமன்பாடுகளில் இடதுபுறம் வார்ப்புரு:Nowrap -ம் வலதுபுறம் r_s² -ம் இருக்கும். அவற்றை ஒரு சமன்பாட்டிலிருந்து மற்றொன்றைக் கழிப்பதன் மூலம் அவற்றிலுள்ள இருபடி உறுப்புகளை நீக்கி, மீதமுள்ள ஒருபடி உறுப்புகளை x_s, y_s இன் மதிப்புகளைத் தருகின்ற நேரியல் சமன்பாடுகளாக பின்வருமாறு மாற்றலாம்.

x_{s} = M + N r_{s}

y_{s} = P + Q r_{s}

இங்கு M, N, P , Q ஆகியவை தரப்பட்ட வட்டங்களின் தெரிந்த அளவுகள் மற்றும் குறிகளின் வாய்ப்புகளாலும் அமையும். இம்மதிப்புகளை முதல் சமன்பாட்டுத் தொகுதியைச் சேர்ந்த ஏதேனும் ஒரு சமன்பாட்டில் பதிலிடக் கிடைக்கும் இருபடிச்சமன்பாட்டைத் தீர்த்து, r_s இன் மதிப்பைக் கண்டுபிடிக்கலாம். பின் r_s இன் எண்மதிப்பை நேரியல் சமன்பாடுகளில் பதிலிடுவதன் மூலம் x_s , y_s மதிப்பினைக் கண்டுபிடிக்கலாம்.

மேற்கோள்கள்

வார்ப்புரு:Reflist

வெளி இணைப்புகள்

வார்ப்புரு:Commons

[Dörrie_1965-1] 1.0 ^1.1 வார்ப்புரு:Cite book

[coxeter_1968-2] வார்ப்புரு:Cite journal

[coolidge-3] 3.0 ^3.1 வார்ப்புரு:Cite book

[coxeter_greitzer-4] வார்ப்புரு:Cite book

[5] வார்ப்புரு:Cite book

[6] வார்ப்புரு:Cite book

[pappus-7] வார்ப்புரு:Cite book வார்ப்புரு:La icon

[bruen_1983-8] வார்ப்புரு:Cite journal

[van_roomen_1596-9] 9.0 ^9.1 வார்ப்புரு:Cite book வார்ப்புரு:La icon

[van_roomen_by_newton-10] 10.0 ^10.1 வார்ப்புரு:Cite book

[Newton_1687-11] வார்ப்புரு:Cite book

[12] வார்ப்புரு:Cite book

[casey_1881-13] வார்ப்புரு:Cite book

[viete_1970-14] 14.0 ^14.1 வார்ப்புரு:Cite book வார்ப்புரு:La icon

[alt_reconstructions-15] Simson R (1734) Mathematical Collection, volume VII, p. 117.
வார்ப்புரு:Cite book வார்ப்புரு:De icon
வார்ப்புரு:Cite book

[16] வார்ப்புரு:Cite journal வார்ப்புரு:Fr icon

[gergonne_1814-17] வார்ப்புரு:Cite journal வார்ப்புரு:Fr icon

[altshiller-court_1961-18] 18.0 ^18.1 வார்ப்புரு:Cite journal

[gabriel-marie_1912-19] வார்ப்புரு:Cite book வார்ப்புரு:Fr icon

[20] வார்ப்புரு:Cite journal வார்ப்புரு:La icon Reprinted in Euler's Opera Omnia, series 1, volume 26, pp. 270–275.

[gauss_1810-21] வார்ப்புரு:Cite book வார்ப்புரு:De icon

[carnot_1803a-22] வார்ப்புரு:Cite book வார்ப்புரு:Fr icon
வார்ப்புரு:Cite book வார்ப்புரு:Fr icon

[23] வார்ப்புரு:Cite journal வார்ப்புரு:Fr icon

[special_cases-24] வார்ப்புரு:Cite book
வார்ப்புரு:Cite book
வார்ப்புரு:Cite book வார்ப்புரு:Fr icon

[coaklay_1860-25] வார்ப்புரு:Cite journal

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

அப்பொலோனியசின் கணக்கு

உள்ளடக்கம்

கூற்று

வரலாறு

தீர்வு முறைகள்