ஆர்க்கிமிடீசின் வளைக்கவராயம்

ஆர்க்கிமிடீசின் வளைக்கவராயத்தின் மாதிரி.

ஆர்க்கிமிடீசின் வளைக்கவராயம் (trammel of Archimedes) என்பது நீள்வட்டத்தை பிறப்பிக்கும் ஒரு இயங்கமைவாகும். வளைக்கவராயத்தில் இரு செங்குத்துத் தடங்களில் கட்டுப்படுத்தப்பட்ட நாடாக்கள் உள்ளன. அவற்றுடன் ஒரு கட்டையானது சுழல்மையங்களைக்கொண்டு கட்டையின் இரண்டு நிலையான இடங்களில் இணைக்கப்பட்டுள்ளது.

நாடாக்கள் அவற்றி தடங்களில் முன்னும் பின்னும் நகரும்போது கட்டையின் மீதுள்ள அனைத்துப் புள்ளிகளும் நீள்வட்டப் பாதையில் நகர்கின்றன. கட்டையின் இயக்கமானது நீள்வட்ட நகர்வு எனப்படுகிறது. இந் நீள்வட்டத்தின் அரை அச்சு நீளங்கள் a, b இரண்டும் கட்டையின் மீதுள்ள புள்ளியிலிருந்து இரு சுழல் மையங்களுக்குள்ள தூரங்களாக இருக்கும்.

சுழல் மையங்கள் உருவாக்கும் நேர்கோடுகள், நீள்வட்டத்தின் சிறப்புவகையாக இருக்கும். இதில், ஒரு அச்சின் நீளம் சுழல்மையங்களுக்கு இடைப்பட்ட தூரத்தைப்போல இருமடங்கும், மற்றொரு அச்சின் நீளம் பூச்சியமாகவும் இருக்கும்.

சுழல்மையங்களுக்கிடைப்பட்ட நடுப்புள்ளியானது அமைப்பின் செங்குத்துத் தடங்கள் சந்திக்கும் புள்ளியை மையமாகக் கொண்ட வட்டப்பாதையில் நகரும். இந்த வட்டமும் நீள்வட்டத்தின் சிறப்புவகையாகவே அமையும். இந்த சிறப்பு நீள்வட்டத்தில் இரு அச்சுகளும் சமநீளமுள்ளவையாக இருக்கும். வட்டப்பாதையின் விட்டம் சுழல்மையங்களுக்கு இடைப்பட்ட தூரமாக இருக்கும். நகர்வின் திசையானது வளைக்கவராயத்தின் சுழல்வின் திசைக்கு எதிரானதாக இருக்கும்.

ஆர்க்கிமிடீசின் வளைக்கவராயத்தின் மரவடிவங்கள், "நீள்வட்டவரைவி" எனப்படும் நீள்வட்டங்கள் வரைவதற்கும் வெட்டி எடுப்பதற்குமான கருவிகளாகப் பயன்படுத்தப்படுகின்றன. மேலும் விளையாட்டுக் கருவிகளிலும் பயன்படுத்தப்படுகிறது.

கணிதம்

ஆர்க்கிமிடீசின் வளைக்கவராயத்தின் வரைபடம்

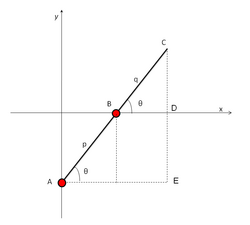
கட்டையின் வெளிமுனை வார்ப்புரு:Mvar;

சுழல்மையங்கள் வார்ப்புரு:Mvar, வார்ப்புரு:Mvar;

வார்ப்புரு:Mvar, வார்ப்புரு:Mvar இரண்டுக்கும் இடைப்பட்ட தூரம் வார்ப்புரு:Mvar;

வார்ப்புரு:Mvar, வார்ப்புரு:Mvar இரண்டுக்கும் இடைப்பட்ட தூரம் வார்ப்புரு:Mvar;

நழுவிகள் வார்ப்புரு:Mvar வார்ப்புரு:Mvar இரண்டும் முறையே வார்ப்புரு:Mvar, வார்ப்புரு:Mvar ஆய அச்சுகளின்மீது நகர்வதாகக் கொள்ளப்படுகிறது;

வார்ப்புரு:Mvar என்பது கட்டையானது x-அச்சுடன் உண்டாக்கும் கோணமெனில், வார்ப்புரு:Mvar புள்ளியின் அச்சுதூரங்கள்:

$x=(AB+BC)\cos \theta$

$y=BC\sin \theta$

இவையிரண்டும் நீள்வட்டத்தின் திட்ட துணையலகுச் சமன்பாடுகளாக உள்ளன. இதிலிருந்து பின்வரும் சமன்பாட்டை எளிதாகப் பெறலாம்:

$\frac{x^2}{(AB+BC{)}^2}+\frac{y^2}{(BC{)}^2}=1$

ஆர்க்கிமிடீசின் வளைக்கவராயமானது இரண்டு நழுவிகள் மற்றும் இரண்டு சுழல்மையங்களுடன் நான்கு தண்டு இயங்கமைவுக்கு ஒரு எடுத்துக்காட்டாக அமைகிறது. மேலும் பொதுவகை சாய்வு வளைக்கவராயத்தின் சிறப்புவகையுமாகவும் உள்ளது. சுழல்மையங்களைக் கட்டுப்படுத்தும் அச்சுகள் செங்குத்தாக இல்லாமலும், வார்ப்புரு:Mvar, வார்ப்புரு:Mvar, வார்ப்புரு:Mvar ஆகிய மூன்று புள்ளிகளும் ஒரு முக்கோணத்தை அமைத்தாலும் வார்ப்புரு:Mvar இன் நகர்வுப்பாதை ஒரு நீள்வட்டமாகவே இருக்கும்.

நீள்வட்டவரைவி

மர நீள்வட்டவரைவி (ca. 1900)

ஜெனிவா நகர அறிவிய வரலாற்று அருங்காட்சியகத்தில் காட்சிப்படுத்தப்பட்டுள்ள நீள்வட்டவரைவி

நீள்வட்டவரைவி என்பது, மரம் அல்லது பிற தகட்டு உலோகங்களிலிருந்து நீள்வட்டங்களை வரைய அல்லது வெட்டியெடுக்கப் பயன்படும் ஆர்க்கிமிடீசின் வளைக்கவராயமாகும். நீள்வட்டவரைவியில் தகுந்த கருவியொன்று (பென்சில், கத்தி போன்றவை) கட்டையுடன் இணைக்கப்பட்டிருக்கும். வெவ்வேறு அளவிலான நீள்வட்டங்களைப் பெறுவதற்கு ஏற்றவாறு a , b இன் அளவுகள் மாற்றிக்கொள்ளக்கூடிய வகையில் அமைந்திருக்கும்.

வட்டவரைவியின் வரலாறு பற்றிய உறுதியான கருத்துக்கள் இல்லையென்றாலும் அது புரொக்கிளசின் காலத்தியதாக (8 பிப்பிரவரி 412 – 17 ஏப்ரல் 485) அல்லது ஆர்க்கிமிடீசின் காலத்தியதாகக் கூட இருக்கலாம் எனக் கருதப்படுகிறது

மேற்கோள்கள்

• J. W. Downs: Practical Conic Sections: The Geometric Properties of Ellipses, Parabolas and Hyperbolas. Courier Dover 2003, வார்ப்புரு:ISBN, pp. 4–5 (வார்ப்புரு:Google books)
• I. I. Artobolevskii Mechanisms for the Generation of Plane Curves. Pergamon Press 1964, வார்ப்புரு:ISBN.

வெளியிணைப்புகள்

• Video of various trammel designs in action
• Cutting ellipses in wood
• Photo of a Kentucky Do-Nothing
• Instructionsவார்ப்புரு:Dead link on how to build a Kentucky Do-Nothing
• Video of a Do-Nothing made from லெகோ bricks
• "Wonky Trammel of Archimedes" வார்ப்புரு:Webarchive An exploration of a generalized trammel.
• US-Patent 4306598 for ellipse cutting guide allowing small ellipses
• Secrets of the Nothing Grinder YouTube video by Mathologer