சம அழுத்தச் செயல்முறை

சம அழுத்தச் செயல்முறை (Isobaric process) அல்லது மாறா அழுத்தச் செயல்முறை என்பது ஒரு தொகுதியின் அழுத்தம் மாற்றமடையாமல் நிலையாக வைத்து நிகழ்த்தப்படும் வெப்பவியக்கவியல் செயல்முறையாகும். இதன் போது தொகுதியினுள் கடத்தப்படும் வெப்பமானது வேலையைச் செய்வதுடன் தொகுதியின் உள்ளாற்றலினையும் அதிகரிக்கிறது:

மஞ்சளினால் சுட்டப்படும் பரப்பு செய்த வேலையை குறிக்கிறது.

$Q=\mathrm{\Delta }U+W$

வெப்பவியக்கவியலின் முதலாவது விதிப்படி W தொகுதியினால் செய்யப்பட்ட வேலையையும், U உள் ஆற்றலினையும், Q தொகுதிக்கு வழங்கிய வெப்பத்தையும் குறிக்கிறது. மூடிய தொகுதியின் கனவளவு - அழுத்த வேலை பின்வருமாறு வரையறுக்கப்படுகிறது:

$W=\int pdV$

இங்கு Δ முழுச்செயல்முறையில் நிகழ்ந்த மாற்றத்தை குறிக்கிறது, d நுண்ணளவைக் குறிக்கிறது. அழுத்தம் மாற்றமடையாது இருப்பதால் இது

$W=p\mathrm{\Delta }V$.

கருத்தியல் வளிம விதியின்படி பின்வருமாறு மாறுகிறது:

$W=nR\mathrm{\Delta }T$

வளிமத்தின் அளவு மாறாதிருக்கும் எனக்கருதுக, உ+ம், நிலைமாற்றம் நிகழாத வேதியியல் தாக்கம். சமபகிர்வுக் கோட்பாட்டின் படி, உள் ஆற்றலில் நிகழும் மாற்றம் தொகுதியின் வெப்பநிலையுடன் தொடர்புடையது

$\mathrm{\Delta }U=n{c}_V\mathrm{\Delta }T$,

இங்கு $c_V$ என்பது மாறாக் கனவளவிலான தன்வெப்பக்கொள்ளளவு.

கடைசி இரண்டு சமன்பாடுகளையும் முதல் சமன்பாட்டில் பிரதியிட வருவது:

$Q=n{c}_V\mathrm{\Delta }T+nR\mathrm{\Delta }T$

$=n(c_V+R)\mathrm{\Delta }T$

$=n{c}_P\mathrm{\Delta }T$,

இங்கு $c_P$ சம அழுத்தத் தன்வெப்பக்கொள்ளளவு.

தன்வெப்பக்கொள்ளளவு

தொடர்புடைய வளிமத்தின் மூலர் தன்வெப்பக்கொள்ளளவை கண்டறிய பின்வரும் சமன்பாடுகள் யாதேனும் பொதுவான கலோரியில் இலட்சியமான வளிமங்களிற்கு பாவிக்கப்படுகின்றன. $\gamma$ தன்வெப்பக்கொள்ளளவு விகிதம் எனப்படுகிறது. சில மூலங்கள் $\gamma$ இற்கு பதிலாக k இனை பயன்படுத்துகின்றன.

மூலர் மாறாக் கனவளவு தன்வெப்பக்கொள்ளளவு:

$c_V=\frac{R}{\gamma -1}$.

மூலர் சம அழுத்த தன்வெப்பக்கொள்ளளவு:

$c_p=\frac{\gamma R}{\gamma -1}$.

$\gamma$ இன் மதிப்பு காற்றிற்கும் அதன் பிரதான கூறுகள் போன்ற ஈரணு வளிமங்களிற்கு $\gamma =1.4$ ஆகவும், இலட்சிய வளிமம் போன்ற ஓரணு வளிமங்களிற்கு $\gamma =\frac{5}{3}$ ஆகவும் உள்ளது. தன் வெப்பக்கொள்ளளவிற்கான கோவைகள் கிழ்க்காணும் சிறப்பு வேளைகளில் பின்வருமாறு ஒடுங்குகிறது:

ஓரணுவிற்கு:

$c_V=\frac{3R}{2}$ மற்றும் $c_P=\frac{5R}{2}$

ஈரணுவிற்கு:

$c_V=\frac{5R}{2}$ மற்றும் $c_P=\frac{7R}{2}$

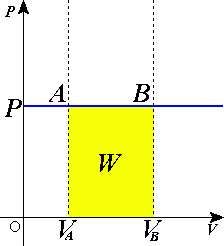
ஓர் சம அழுத்த செயல்முறை P-V வரைபடத்தில் இறுதி ஆரம்ப நிலைகளை கிடையான நேர்கோட்டால் இணைத்துக் காட்டப்பட்டிருக்கும். இங்கு செயல்முறை வலது பக்கத்தை நோக்கி நகருமாயின் அது விரிவடைதல் என்றும் இடது பக்கத்தை நோக்கி நகருமாயின் அது நெருங்குதல் என்றும் அழைக்கப்படும்.

வேலைக்கான குறி வழக்கு

வெப்பவியக்கவியலின் குறித்த குறி வழக்கிற்கான உந்துகை வெப்ப பொறிகளின் ஆரம்பகால முன்னேற்றத்துடன் வந்தது. வெப்ப பொறிகளினை வடிவமைக்கையில் இலக்காக இருப்பது வேலையை வெளியீடாக விடுவதற்கான அமைப்பினை உருவாக்குதலாகும். வெப்ப பொறியின் ஆற்றல் மூலமாக அமைவது வெப்பம் வளங்குதலாகும்.

கனவளவு நெருக்கப்படும் போது (டெல்டா V = இறுதிக்கனவளவு-ஆரம்பக் கனவளவு < 0), ஆகவே W < 0. அதாவது சம அழுத்த செயல்முறையில் வளிமம் எதிர்ம வேலையை செய்கிறது அல்லது சூழல் வளிமம் மீது நேர் வேலையைச் செய்கிறது.

கனவளவு விரிவாக்கப்படுகையில் போது (டெல்டா V = இறுதிக்கனவளவு-ஆரம்பக் கனவளவு > 0), ஆகவே W > 0. அதாவது சம அழுத்த செயல்முறையில் வளிமம் நேர்ம வேலையை செய்கிறது அல்லது சூழல் வளிமம் மீது எதிர்ம வேலையைச் செய்கிறது.

தொகுதிக்கு வெப்பம் சேர்க்கப்படுமாயின் Q > 0 ஆகும். அதாவது மாறா அமுக்கத்தில் விரிவடைதல் அல்லது வெப்பப்படுத்தும் போது நேர் வெப்பம் வளிமத்திற்கு சேர்க்கப்படுகிறது அல்லது நிகராக எதிர்ம வெப்பத்தை சூழல் பெறுகிறது. மீளக்கூறுவதாயின் வளிமம் சூழலில் இருந்து நேர் வெப்பத்தை பெறுகிறது.

தொகுதிக்கு வெப்பத்தை இழக்குமாயின் Q < 0 ஆகும். அதாவது மாறா அமுக்கத்தில் நெருக்குதல் அல்லது குளிர்விக்கும் போது எதிர்ம வெப்பம் வளிமத்திற்கு சேர்க்கப்படுகிறது அல்லது நிகராக நேர்ம வெப்பத்தை சூழல் பெறுகிறது. மீளக்கூறுவதாயின் சூழல் வளிமத்திலிருந்து நேர் வெப்பத்தை பெறுகிறது.

வெப்ப அடக்கத்தினை வரையறுத்தல்

ஓர் மாறாக்கனவளவு செயல்முறை $Q=\mathrm{\Delta }U$ எனும் சமன்பாட்டால் விபரிக்கப்படுகிறது. ஆனால் சமஅழுத்தச் செயல்முறையில்

$Q=\mathrm{\Delta }U+\mathrm{\Delta }(pV)=\mathrm{\Delta }(U+pV)$

U + p V என்பது செயன்முறையின் நிலையுடன் தொடர்புடைய கணியம், எனவே இதை ஓர் பெயர் கொண்டு அழைக்க முடியும். இது வெப்ப அடக்கம் (enthalpy) என்று அழைக்கப்படுகிறது, H என்பதைல் குறிக்கப்படுகிறது. ஆகவே சம அழுத்த செயல்முறையை

$Q=\mathrm{\Delta }H$.

எனும் சமன்பாட்டால் விபரிக்கமுடியும்.

வெப்ப அடக்கமும் மாறாக்கனவளவு தன் வெப்பக்கொள்ளளவும் திறந்த தொகுதி செயல்முறையை ஆராய்கையிலும், மாறாக்கனவளவில் பூச்சிய வேலை நடைபெறும் சந்தர்ப்பங்களிலும் பயனுள்ள கணித கட்டமைப்புக்களாக இருக்கின்றன. ஒர் திறந்த தொகுதியில் வெப்ப அடக்கமானது பாய்மம் கொண்டுள்ள ஆற்றலின் அளவை கண்காணிப்பதற்கான பயனுள்ள கணியமாக உள்ளது.

மாறும் அடர்த்தி பற்றிய கண்ணோட்டம்

மாறுபடும் கனவளவுடைய குறித்த அளவு (திணிவு m) வளிமம் மாறும் அடர்த்தி ρ இனை தருகிறது. இப்பின்னணியில் இலட்சிய வளிம விதியானது பின்வருமாறு எழுதப்படுகிறது

R(T ρ) = M P

இங்கு T என்பது வெப்பவியக்கவியல் வெப்பநிலை. R மற்றும் M மாறிலியாக இருக்கையில், அமுக்கம் P can stay constant as the density-temperature quadrant (ρ,T ) undergoes a squeeze mapping.