வில்லை (ஒளியியல்)

உருப்பெருக்கிக் கண்ணாடியில் உள்ள வில்லை. இது இருகுவி வில்லை ஆகும். இவ்வகை வில்லைகள் கதிரொளியை குவியச்செய்து வெப்பச் செறிவால் (அடர்த்தியால்) காய்ந்த இலை, பஞ்சு, காகிதம் போன்றவற்றைத் தீப்பற்றச் செய்யவல்லது.

ஒளியைக் குவியப்படுத்த வில்லைகள் பயன்படுகின்றன.

ஒரு இருபக்க குவி வில்லை

வில்லை (lens) என்பது ஒளிக் கதிர்களைக் குறிப்பிட்டவாறு குவிக்கவோ அல்லது விரியவோ செய்யவல்ல ஓர் எளிய கருவி. இது ஒரு பொருளை பெரிதாகவோ அல்லது சிறிதாகவோ காட்ட வல்லது. பொதுவாக ஒற்றை வில்லைகள் கண்ணாடி அல்லது நெகிழி போன்ற ஒளி ஊடுருவும் பொருளால் செய்யப்பட்டது. இரட்டை வில்லை, மும்மை வில்லை போன்றவை பல ஒற்றை வில்லைகளை ஒரே அச்சில் அமைப்பதன் மூலம் உருவாக்கப்படுகிறது. ஒளி ஓர் ஊடகத்தில் இருந்து வேறு ஓர் ஊடகத்தின் வழியே செல்லும் பொழுது ஏற்படும் ஒளிவிலகல் பண்பே வில்லையின் அடிப்படைப் பண்பாகும். இதன் அடிப்படையிலேயே வெவ்வேறு வளைவுகளைக் கொண்ட வில்லையின் பரப்புகள் அமைக்கப்படுகின்றன. ஒரு வில்லையின் புறப் பரப்புகள் சீரான குழியாகவோ, குவிந்தோ அல்லது சமதளமாகவோ இருக்கும்.

வெளிநோக்கி வளைந்து குவிந்து இருந்தால் குவிப் பரப்பு என்றும், உள்நோக்கி வளைந்து குழிந்து இருந்தால் குழிப் பரப்பு என்றும், நேரான சமதளமாக இருந்தால் சமதளப் பரப்பு என்றும் குறிக்கப்படும். ஒருபுறம் ஒளி நுழைந்து மறுபுறம் ஒளி வெளி வருமாகையால் வில்லைக்கு இரு பரப்புகளும் முக்கியமானவை.

பட்டகம், ஒரு ஒளிக் கதிரை விலகலடைய மட்டுமே செய்யும், ஆனால் வில்லைகள் ஒளியை விலகலடையச் செய்வதோடு, அவற்றை குவித்து பிம்பங்களையும் உருவாக்க வல்லது. நுண்ணலைகளை குவிக்கும் வில்லைகள் மற்றும் இலத்திரன்களை குவிக்கும் வில்லைகள் என கண்ணுக்குப் புலனாகாத கதிர்களையும் குவிக்கும் வில்லைகளும் உள்ளன.

வில்லை என்பது பெரும்பாலும் திண்மப் பொருட்களால் ஆனது என்றாலும், தாமரை இலையின் மீது உள்ள நீரும், பனித்துளியும் திரண்டு புறப் பரப்பு குவிந்து இருப்பதால் அவைகளும் வில்லையின் பணியையே செய்கின்றது. மெல்லிய அட்டை போன்ற ஒரு தட்டையான ஒளியூடுருவு பொருளும் குறிப்பிட்ட சில வழிகளில் கீறப்பட்டோ வடிவமைக்கப்பட்டோ இருந்தால் அவைகளும் வில்லை போல இயங்க வல்லன (பார்க்க ஃவிரெனெல் வில்லை). ஒளிப்படக்கருவி, நுண்நோக்கி போன்ற பல அன்றாடக் கருவிகளிலும் அறிவியல் ஆய்வுக் கருவிகளிலும் வில்லை பரவலாக பயன்படுகின்றது.

வரலாறு

நிம்ரூட் வில்லை

(வில்லை) lens என்ற ஆங்கிலச் சொல், இலத்தீன் மொழியில் lentil (மைசூர்ப் பருப்பு) என்ற சொல்லிருந்து பெறப்பட்டது. இருபக்க குவிவில்லை பருப்புகளைப் போன்ற அமைப்பைப் பெற்றிருப்பதால் இப் பெயர் பெற்றது. புதை பொருள் ஆராய்ச்சியாளர்கள், வில்லைகள் பல நூற்றாண்டுகளுக்கு முன்பே உருவாக்கப்பட்டது என்கின்றனர். 7வது நூற்றாண்டிலேயே பாறைப்பளிங்குகளைக் (rock crystal) கொண்டு நிம்ரூட் வில்லைகள் (Nimrud lens) உருவாக்கபட்டதாகவும், அவைப் பொருளை உருப்பெருக்கவோ அல்லது ஒளியைக் குவித்து ஒரு பொருளை எரிக்கவோ பயன்படுத்தாகவும் சான்றுகள் கூறுகின்றன.

கி பி 424 ல் அரிஸ்டாஃபனீஸ் எழுதிய மேகங்கள் (The Clouds) என்ற நாடகத்தில் எரிக்கும் வில்லைகளைப் பற்றி கூறியுள்ளார். மூத்த பிளினி எழுதிய இயற்கை வரலாறு நூலில் (The Natural History) (trans. John Bostock) Book XXXVII, Chap. 10.</ref> வரும் நீரோ என்ற கதாபத்திரம் மரகதக் கல்லைக் கொண்டு, தனது கிட்டப்பார்வையை சரி செய்ததாக எழுதியுள்ளார். இரண்டாம் நூற்றாண்டைச் சேர்ந்த தொலெமி ஒளியியல் தொடர்பான புத்தகம் எழுதியுள்ளார். 11 ஆம் நூற்றாண்டிலிருந்து 13 ஆம் நூற்றாண்டு வரை கோளக கண்ணாடிகளை வெட்டி, படிக்கும் கண்ணாடிகளை உருவாக்கினர். 12 ஆம் நூற்றாண்டில் பாறைபளிங்குகளை பயன்படுத்தி எரிக்கும் வில்லைகளை உருவாக்கினர். 13 ஆம் நூற்றாண்டில் பாறைப்பளிங்குகளை பயன்படுத்தி தண்ணாடிகள் தயாரிக்கப்பட்டது. 13 ஆம் நூற்றாண்டில் வெனிசு மற்றும் புளோரன்சு நகரங்களில் கண்ணாடிகளை அரைத்து, பளபளப்பாக்கும் தொழிற்சாலைகள் தொடங்கப்பட்டன. பின்னர் நெதர்லாந்து மற்றும் செர்மனியில் மூக்குக் கண்ணாடிகளை உருவாக்கும் தொழிற்சாலைகள் தொடங்கப்பட்டன. பார்வைக் கோளாறைச் சரி செய்யும் மூக்குக் கண்ணாடிகளும் தயாரிக்கப்பட்டது. இதைத் தொடர்ந்து 1595 ல் கூட்டு ஒளியியல் நூண்நோக்கிகளும், 1608 ல் ஒளிவிலகல் வகை தொலைநோக்கிகளும் உருவாக்கப்பட்டன.

ஒற்றை வில்லைகளை உருவாக்குதல்

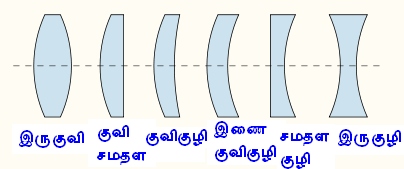
வில்லைகள் பொதுவாக கோள வடிவமானது. அவையனைத்தும் கோளத்தின் ஒரு பகுதியாகவே உள்ளது. இருகுவி வில்லை என்பது இருபரப்பும் குவிந்திருக்கும் வில்லை ஆகும். அதே போல இரு பரப்பும் குழிந்து இருந்தால் இருகுழி வில்லை எனப்படும். ஒரு பரப்பு, குவிந்தும் ஒரு பரப்பு சமதளமாகவும் இருந்தால் குவிசமதள வில்லை எனப்படும். ஒரு பரப்பு குழிந்தும் மறு பரப்பு சமதளமாகவும் இருந்தால் குழிசமதள வில்லை எனப்படும். ஒருபரப்பு குவிந்தும், மறுபரப்பு குழிந்தும் இருந்தால் குவிகுழி வில்லை எனப்படும். ஒரு குவிகுழி வில்லையின் வளைவுகள் ஒரே அளவான உருண்டைப் பரப்பாக இருக்குமானால் அதனை இணை குவிகுழி வில்லை என்பர்..

கோளக-உருளை வில்லைகள் (Toric lens) என்பவை வெவ்வேறு அச்சுகளில் வெவ்வேறு குவியத்திறனைப் (focal power) பெற்றிருக்கும். இவ்வகை வில்லைகள் சிதறல் பார்வையைச் சரிசெய்ய உதவுகிறது.

கோளவுருவில்லாத வில்லைகள் (aspheric lens) கோள வடிவமோ அல்லது உருளை வடிவமோ கொண்டிருப்பதில்லை. இவை ஒளிப்பிறழ்ச்சிகளைக் (Optical aberration) களைய பயன்படுகிறது.

வில்லைகளின் வகைகள்

பொதுவாக வில்லையின் (லென்ஸ்) புறப்பரப்பின் வளைவானது குவிந்து இருந்தாலும், குழிந்து இருந்தாலும் உருண்டை உருவின் புறப் பரப்பை ஒத்து இருக்கும். வில்லையின் இரு பரப்புகளும் எவ்வகையானது என்பதைப் பொருத்து, ஒளிக்கதிர்களை அது திசை திருப்பும் பண்பு அமையும். இருகுவி வில்லை என்பது இருபரப்பும் குவிந்திருக்கும் வில்லை ஆகும். அதே போல இரு பரப்பும் குழிந்து இருந்தால் இருகுழி வில்லை எனப்படும். ஒரு பரப்பு, குவிந்தும் ஒரு பரப்பு சமதளமாகவும் இருந்தால் குவிசமதள வில்லை எனப்படும். ஒரு பரப்பு குழிந்தும் மறு பரப்பு சமதளமாகவும் இருந்தால் குழிசமதள வில்லை எனப்படும். ஒருபரப்பு குவிந்தும், மறுபரப்பு குழிந்தும் இருந்தால் குவிகுழி வில்லை எனப்படும். ஒரு குவிகுழி வில்லையின் வளைவுகள் ஒரே அளவான உருண்டைப் பரப்பாக இருக்குமானால் அதனை இணை குவிகுழி வில்லை என்பர். இவ்வகைகளைக் கீழ்க்கண்ட படத்தில் காணலாம்

இருகுவி அல்லது குவிசமதள வில்லைகளின் மீது படும் இணைகதிர் கற்றை, வில்லைகளை ஊடுறுவிச் சென்று முக்கிய குவியத்தில் குவிக்கப்படும். இவ்வகை வில்லைகள் நேர்மறை அல்லது குவிக்கும் வில்லைகள் எனப்படுகிறது. இதில் f என்பது குவியத் தூரம் ஆகும்.

இருகுவிவு வில்லை

வில்லை இருகுழி வில்லையாகவோ அல்லது சமதள குழி வில்லையாகவோ இருந்தால், இணையாக வரும் ஒளிக்கற்றை வில்லைகளை கடந்த பின் பிரிந்து செல்லும். பாதி ஒளிக்கற்றைகள் வில்லைகளுக்கு முன்னரே ஒரு இடத்தினில் குவிக்கப்படும். அப்படி குவிக்கப்பட்டால் அவை எதிர்மறை அல்லது விரிக்கும் குழிவில்லை எனப்படும். வில்லைக்கும் குவிப் புள்ளிக்கும் இடையில் உள்ள தூரம் குவியத்தொலைவு (focal length) எனப்படும்.

இருகுழிவு வில்லை

பொதுவாக 'இருபுற குவிவுவில்லை' என்பதனை குவிவுவில்லை என்றே குறிப்பிடலாம். குவிவுவில்லை மையங்களில் தடித்தும், ஓரங்களில் மெலிந்தும் காணப்படும்.

ஒளிவில்லையாளரின் சமன்பாடு

காற்று ஊடகத்தில் வில்லையின் குவியத்தூரம் காண ஒளிவில்லையாளரின் சமன்பாடு ஆகும்:

$\frac{1}{f}=(n-1)[\frac{1}{R_1}-\frac{1}{R_2}+\frac{(n-1)d}{n{R}_1{R}_2}],$

இதில்

$f$ என்பது வில்லையின் குவியத்தூரம்,

$n$ என்பது வில்லையின் ஒளிவிலகல் எண்,

$R_1$ என்பது ஒளி மூலத்தின் அருகிலுள்ள வில்லைப் பகுதியின் வளைவு ஆரம்,

$R_2$ என்பது ஒளி மூலத்தின் தொலைவிலுள்ள வில்லைப் பகுதியின் வளைவு ஆரம், மற்றும்

$d$ என்பது வில்லையின் தடிமன்.

f என்பது குவிக்கும் வில்லைக்கு நேர்மறையாகவும், விரிக்கும் வில்லைக்கு எதிர்மறையாகவும் இருக்கும். குவியத்தூரத்தின் பெருக்கல் நேர்மாறு 1/f என்பது வில்லையின் குவியத்திறன் ஆகும். குவியத்தூரம் என்பது மீட்டரில் அளக்கப்படுகிறது. குவியத்திறன் என்பது டையாப்ட்டரில் அளக்கப்படுகிறது

வில்லைகளின் குவியத்தூரம், வில்லை வழியாக ஒளிச் செல்லும் பாதையைப் பொறுத்து மாறுவதில்லை. ஆனால் ஒளியின் மற்ற பண்புகள் ஒளிச் செல்லும் பாதையைப் பொறுத்து மாறுபடும்.

R₁ மற்றும் R₂ ஆகிய வளைவு ஆரங்களின் குறியீட்டு மரபு

வளைவு ஆரங்களின் குறியீடு, அவை குவி வில்லையா அல்லது குழி வில்லையா என்பதை நிர்ணயிக்கும். குறியீட்டு மரபு (sign convention) இதை நிர்ணயிக்கப் பயன்படுகிறது. ஒளி செல்லும் திசையில் வளைவு ஆரம் R இருந்தால், அதாவது இனி மேல் தான் பரப்பின் வளைவு மையத்தைக் கடக்கும் எனில், அது நேர்மறை குறியீட்டைப் பெறும். பரப்பின் வளைவு மையத்தைக் கடந்து மறுபக்கத்தை ஒளி அடைந்திருந்தால், அந்த பரப்பின் வளைவு ஆரம் R எதிர்மறை குறியீட்டைப் பெறும். இதன் படி வார்ப்புரு:Nowrap குவிந்த பக்கங்கள் நேர்மறை குறியீட்டையும் மற்றும் வார்ப்புரு:Nowrap குழிந்த பக்கங்கள் எதிர்மறை குறியீட்டையும் பெறும். சமதள பக்கங்களின் ஆரம் முடிவிலியாக இருக்கும்.

மென்வில்லை சமன்பாடு

R₁ மற்றும் R₂ ஒப்பிடும் போது d மிகச் சிறியதாக இருந்தால் அதை மென்வில்லை என்கிறோம். காற்று ஊடகத்தில் அதன் f மதிப்பு

$\frac{1}{f}\approx (n-1)[\frac{1}{R_1}-\frac{1}{R_2}].$வார்ப்புரு:Sfn

பிம்பங்களை உருவாக்கும் பண்புகள்

மேலே குறிப்பிட்ட படி, காற்று ஊடகத்தில் நேர்மறை அல்லது குவிக்கும் வில்லை வழியாகச் செல்லும் ஒளிக்கதிர், ஒளி விலகலுக்குப் பின், மைய அச்சிலுள்ள f என்ற முக்கிய குவியத்தில் குவியும். இதற்கு மாறாக முக்கிய குவியத்தில் ஒளி மூலத்தை வைக்கும் போது, ஒளி விலகலுக்குப் பின் இணை கற்றைகளை உருவாக்கும். இந்த நிலையில் குவியத்தூரம் முடிவிலியாக இருக்கும்.

S₁ என்பது பொருளிலிருந்து வில்லை வரை உள்ள தூரம், S₂ என்பது பிம்பத்திலிருந்து வில்லை வரை உள்ள தூரம் ஆகும். மென்வில்லை சமன்பாடு:

$\frac{1}{S_1}+\frac{1}{S_2}=\frac{1}{f}$ .

அதே சமன்பாடு நியூட்டனின் அமைப்பில்:

$x_1{x}_2=f^2,$வார்ப்புரு:Sfn

இதில் $x_1=S_1-f$ மற்றும் $x_2=S_2-f$.

தூரத்திலுள்ள பொருளின் மெய்ப் பிம்பத்தை உருவாக்கும் புகைப்படக்கருவி வில்லை ஒன்று.

பொருளை வார்ப்புரு:Nowrap என்ற தூரத்தில் வைக்கும் போது, வில்லையின் மறுபக்கத்தில் S₂ என்ற தூரத்தில் மெய்ப் பிம்பத்தைப் பெறலாம். இது திரையில் பெறக் கூடிய பிம்பம் ஆகும்.

உருப்பெருக்கும் வில்லையனால் உருவாக்கப்படும் மாயபிம்பம்.

மனிதக் கண்ணும் புகைப்படக்கருவியும் ஒரே தத்துவத்தில் செயல்படுகிறது.

குழி வில்லைகளில் S₂ என்பது எதிர்மறை தூரமாக உள்ளது. இதில் பிம்பமானது, குவியத்திலிருந்து விரிந்து வருவது போல் தோற்றமளிக்கும். இவ்வகை பிம்பங்கள் திரையில் பிடிக்க இயலாத மாய பிம்பங்களாக இருக்கும். உருப்பெருக்கும் கண்ணாடி இத் தத்துவத்திலே செயல்படுகிறது.

வார்ப்புரு:Multiple image

குழி வில்லை உருவாக்கும் மாய பிம்பத்தை மீண்டும் மெய் பிம்பமாக மாற்ற பர்லோ வில்லை (Barlow lens) பயன்படுகிறது.

வார்ப்புரு:Multiple image

மென் வில்லைகளில் இதே போன்ற (S₁ மற்றும் S₂) தூர அளவீடுகளே பயன்படுத்தப்படுகின்றன. ஆனால் கூட்டு வில்லைகளில் தூர அளவீடுகள் எளிமையாக இருப்பதில்லை.

உருப்பெருக்கம்

ஒற்றை வில்லைகளின் உருப்பெருக்கம் காணும் சமன்பாடு:

$M=-\frac{S_2}{S_1}=\frac{f}{f-S_1}$ ,

இதில் M என்பது உருப்பெருக்கம். இது பிம்பத்தின் அளவையும் பொருளின் அளவையும் வகுக்க கிடைக்கிறது. குறியீட்டு மரபின் படி, தலை கீழ் அல்லது மெய் பிம்பங்களுக்கு, M நேர்மறையாகவும், நேரான அல்லது மாய பிம்பங்களுக்கு, M எதிர்மறையாகவும் எடுத்துக்கொள்ளப்படுகிறது.

பிறழ்ச்சிகள்

வில்லைகள் சரியான படங்களை உருவாக்குவதில்லை. அவற்றில் சில இடங்களில் விலகல் மற்றும் பிறழ்ச்சிகள் ஏற்படுகின்றன. வில்லைகளை சரியாக தயாரிப்பதன் மூலமே இதனை ஒரளவிற்கு சரி செய்ய இயலும். பிறழ்ச்சியில் பல வகைகள் உள்ளன.

கோளப் பிறழ்ச்சி

வில்லைகளில் கோள அமைப்பு மாறுபடுவதால் இவ்வகை பிறழ்ச்சி ஏற்படுகிறது. இது பெரும்பாலும் குவி வில்லையில் ஏற்படக்கூடிய பிறழ்ச்சி ஆகும். இவ்வகை பிறழ்ச்சியால் பிம்பங்கள் முதன்மை அச்சை விட்டு விலகி குவி்க்கப்படும். அதனால் பிம்பங்கள் தெளிவாக அமைவதில்லை. கோளவுருவில்லாத வில்லைகளே (aspheric lens) இதற்குக் காரணம். வளைவு பரப்புகளை சரியாக அமைப்பதன் மூலம் கோளப் பிறழ்ச்சியை சரி செய்யலாம்

வால் பிறழ்ச்சி (Coma aberration)

இதுவும் குவி வில்லையில் ஏற்படுகின்ற ஒரு பிறழ்ச்சியே ஆகும். இப்பிறழ்ச்சியினால் ஏற்படும் பிம்பம், வால்வெள்ளியின் வடிவத்தில் இருப்பதனால் இதற்கு கோமா பிறழ்ச்சி என்று பொயர் ஏற்பட்டது. இவ்வகை பிறழ்ச்சியால் ஒளிக் கதிர்கள் வெவ்வேறு புள்ளிகளில் குவிக்கப்படுகிறது. முதன்மை அச்சுக்கு தொலைவில் குவிக்கப்பட்டால் அது நேர்மறை கோமா எனவும், அருகில் குவிக்கப்பட்டால் எதிர்மறை கோமா எனவும் அழைக்கப்படுகிறது. வளைவு பரப்புகளை சரியாக அமைப்பதன் மூலம் கோமா பிறழ்ச்சியை சரி செய்யலாம்

நிற பிறழ்ச்சி (chromatic aberration)

வெவ்வேறு ஒளிவிலகல் குறிப்பெண்கள் கொண்ட ஒளிக்கதிர்கள் வெவ்வேறு அளவில் நிறப்பிரிகை அடைவதால், இப்பிறழ்ச்சிகள் ஏற்படுகின்றன. இப்பிறழ்ச்சியினால் வெவ்வேறு நிறங்களின் குவி புள்ளி வெவ்வேறு இடங்களில் இருக்கும். இதனால் நிறங்கள் பிரிக்கப்படுகின்றன. நிறப்பிறழ்ச்சி இல்லா வில்லைகளைப் பயன்படுத்துவதன் மூலம் இவ்வகை பிறழ்ச்சிகள் சரி செய்யப்படுகின்றன. அதிக அபி எண் கொண்ட புளோரைட் படிகங்களால் ஆன வில்லைகளும் இவ்வகை பிறழ்ச்சிகள் குறைக்கின்றன.

கூட்டு வில்லைகள்

பிறழ்ச்சிகளைத் தவிர்க்க கூட்டு வில்லைகள் (compound lens) பயன்படுகின்றன. ஒரே அச்சில் அமையும் இரண்டு அல்லது அதற்கு மேற்பட்ட வில்லைகளால் இவை உருவாக்கப்படுகின்றன.

f1 மற்றும் f2 ஆகிய குவியத் தூரங்களைக் கொண்ட இரு மென் வில்லைகள் உருவாக்கும் கூட்டு வில்லையின் குவியத் தூரம்:

$\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}.$

பயன்பாடுகள்

• குவி வில்லைகள் பொருள்களை பெரிதுபடுத்தி பார்க்க உதவுகிறது. மூக்கு கண்ணாடிகள் செய்ய வில்லைகள் பயன்படுகின்றன.
• தொலைநோக்கி, நுண்ணோக்கி, புகைப்படக்கருவி, இருகண் நோக்கி, ஆகியவற்றில் வில்லைகள் பிரதானமாக பயன்படுகின்றன.
• கிட்டப்பார்வை, எட்டப் பார்வை, மூப்புப்பார்வை, சிதறல் பார்வை ஆகியவற்றை சரி செய்யவும் வில்லைகள் பயன்படுகின்றன.

மேலும் பார்க்க

• போக்கா
• கண்வில்லை
• குவிய விகிதம்
• ஈர்ப்பு வில்லை
• ஒளியால் நிறம் மாறும் கண்ணாடிகள்
• பட்டகம்

உசாத்துணைகள்

• வார்ப்புரு:Cite book Chapters 5 & 6.
• வார்ப்புரு:Cite book
• வார்ப்புரு:Cite book

வெளியிணைப்புகள்

• Applied photographic optics Book
• The properties of optical glass
• Handbook of Ceramics, Glasses, and Diamonds
• Optical glass construction
• History of Optics (audio mp3) by Simon Schaffer, Professor in History and Philosophy of Science at the University of Cambridge, Jim Bennett, Director of the Museum of the History of Science at the University of Oxford and Emily Winterburn, Curator of Astronomy at the National Maritime Museum (recorded by the பிபிசி).
• a chapter from an online textbook on refraction and lenses வார்ப்புரு:Webarchive
• Thin Spherical Lenses on Project PHYSNET.
• Lens article at digitalartform.com வார்ப்புரு:Webarchive
• Article on Ancient Egyptian lenses
• picture of the Ninive rock crystal lens வார்ப்புரு:Webarchive
• Do Sensors “Outresolve” Lenses? வார்ப்புரு:Webarchive; on lens and sensor resolution interaction.
• Fundamental optics வார்ப்புரு:Webarchive
• FDTD Animation of Electromagnetic Propagation through Convex Lens (on- and off-axis) on YouTube
• The Use of Magnifying Lenses in the Classical World
• Learning by Simulations – Concave and Convex Lenses
• OpticalRayTracer – Open source lens simulator (downloadable java)
• Video with a simulation of light while it passes a convex lens
• Animations demonstrating lens by QED