வெப்பச் சமன்பாடு

சாதாரண வெப்பநிலையில் இருக்கும் ஒரு இரும்புத்தட்டு காய்ச்சிவிடப்பட்டால், காய்ச்சப்பட்ட பகுதி நேரம் செல்லச் செல்ல தன் அதிகரித்த வெப்பநிலையில் இருந்து குறையத் தொடங்கும். இது முனையில் ஆரம்பித்து உள்நோக்கி நகரும். காய்ச்சப்பட்ட பகுதிக்கு வெளியே உள்ள பகுதியின் வெப்பநிலை மெல்ல மெல்ல அதிகரிக்கத் தொடங்கும். இறுதியாக, தட்டின் முழுப்பகுதியும் சீரான சம வெப்பநிலையை அடையும். இருபரிமாணத்தில் உள்ள வெப்பச் சமன்பாட்டைக் கொண்டு இவ்வெப்பப் பரவலை அறியலாம். இந்த விளக்கப்படத்தில், நிறமும் உயரமும் வெப்பநிலையைக் காட்டப் பயன்படுத்தப்பட்டுள்ளன.

வெப்பச் சமன்பாடு (Heat equation) என்பது ஒரு பொருளிலோ, பரப்பிலோ, பகுதியிலோ வெப்பப்பரவலைக் காட்டப் பயன்படும் ஒரு சமன்பாடு ஆகும். இது ஒரு பரவளைய பகுதிவகைக்கெழுச் சமன்பாடாக, அப்பகுதியில் நேரத்தைப் பொறுத்து வெப்பநிலையில் ஏற்படும் மாறுபாட்டை விளக்குகிறது.

சமன்பாடு

ஒற்றைப் பரிமாணக் கம்பியொன்றின் பக்கங்கள் குறித்த நிலையான வெப்பநிலையைக் கொண்டிருக்கும்போது (இங்கே, முறையே 0.8 மற்றும் 0 என்னும் மதிப்பு) அது தொடக்கத்தில் பரவளைவு வடிவத்தில் இருந்து, நேரத்தைப் பொறுத்து நேர்ச்சார்பு போல ஆகிவிடுதலைக் காட்டும் படம்.

$x,y,z$ என்பவை இடத்தைக் குறிக்கும் மாறிகளாகவும் (பார்க்க: கார்ட்டீசியன் ஆய முறைமை) $t$ என்பது நேரத்தைக் குறிக்கும் மாறியாகவும் இருக்கும்போது, $u(x,y,z,t)$ என்ற சார்பின் வெப்பச் சமன்பாடு,

$\frac{\partial u}{\partial t}-\alpha (\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2})=0$

என்பதாக இருக்கும். இதையே பொதுவில் (எந்தவொரு ஆள்கூற்று முறைமைக்கும் பொருந்துமாறு கீழ்க்கண்டவாறு எழுதலாம்.

$\frac{\partial u}{\partial t}-\alpha {\mathrm{\nabla }}^{2}u=0$

இங்கு α என்பது மிகை மாறிலியாகும், Δ அல்லது ∇^2 என்பது லேப்லாசுக் குறியீடு. வெப்பநிலைப் பரவல் குறித்த சமன்பாடு எனில், α என்பது வெப்பப் பரவல் திறன் ஆகும். இதில், u(x,y,z,t ) என்பது வெப்பச்சார்பு ஆகும்.

பொதுவிளக்கம்

ஒற்றைப் பரிமாண பகுதிவகைக்கெழு வெப்பச் சமன்பாட்டின் தீர்வு. தொடக்கத்தில், வெப்பநிலை (u) ஓரலகு நீள இடைவெளியில் பரவியிருக்கிறது. (x = [0,1]). இதன் முனைகள் வெப்பக் காப்பு செய்யப்பட்டிருக்கிறது. இப்பரவலானது நேரம் செல்லச் செல்ல ஒரு சமநிலையை அடைகிறது.

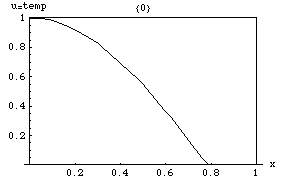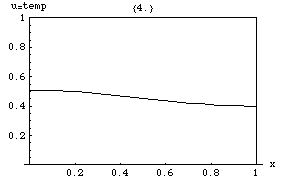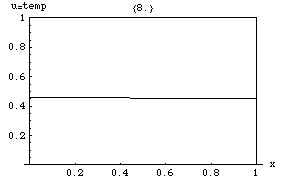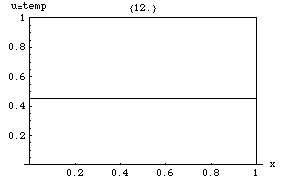
$u$ என்னும் சார்பு ஒன்று $(x,y,z)$ என்னும் இடத்தின் வெப்பநிலையை விவரிக்கிறது எனில், இச்சார்பு நேரத்தைப் பொறுத்து வெப்ப மாறுபாட்டிற்கேற்றவாறு மாறிக்கொண்டேயிருக்கும். நேரத்தில் இந்த வெப்ப மாறுபாட்டு அளவினைக் கணக்கிட வெப்பச் சமன்பாடு பயன்படுகிறது. $u(x,y,z,t)$ சார்பின் மாறுபாட்டு விகிதம் u வளைவரையின் மாறுபாட்டு விகிதத்திற்கு நேர்விகிதத்தில் இருக்கும்.

வலதுபுறம் உள்ள படத்தில் ஒரு இரும்புப் பட்டையில் வெப்பமாற்றம் நிகழ்வது காட்டப்பட்டுள்ளது. வெப்பச் சமன்பாட்டின் சுவையான பண்பு ஒன்று - மிகுமக் கோட்பாடு - u - இன் அதிகபட்ச மதிப்பானது, பரப்பின் முனைபுள்ளியிலோ அல்லது கணக்கிடக் குறைந்த நேரத்திலோ அமையும் என்கிறது. வெப்பமானது வெப்ப மூலத்திலோ அல்லது தொடக்க நேரத்திலோ கிடைக்கப்பெறும் என்று இது காட்டுகிறது. ஏனெனில் வெப்பமானது பரவும், ஆனால் அதை ஒன்றுமில்லாமல் உருவாக்க இயலாது. இப்பண்பு பரவளைய வகைகெழுச்சமன்பாட்டின் பயன்பாடு ஆகும்.

இயற்பியல் சமன்பாடு

ஒரு பரிமாணச் சமன்பாடு

வெப்பச் சமன்பாடானது பூரியர் விதி மற்றும் ஆற்றல் காப்பு விதியிலிருந்து பெறப்படுகிறது. அதாவது, ஒரலகு பரப்பில் உள்ள வெப்ப மாறுபாட்டு விகிதமானது, மொத்தப் பரப்பில் வெப்பச் சார்பின் எதிர்மதிப்பிற்கு, நேர்விகிதத்தில் அமையும்.

$𝐪=-k\mathrm{\nabla }u$

இங்கு $k$ என்பது வெப்பக் கடத்துதிறன் ஆகவும், $u$ வெப்பநிலையாகவும் அமையும். ஒற்றைப் பரிமாணத்தில்,

$q=-k\frac{\partial u}{\partial x}$.

என்று அமையும்.

முப்பரிமானச் சமன்பாடு

முப்பரிமான வெளியில் உள்ள ஒருபடித்தான ஊடகத்தில் வெப்ப அலைபரவல் சமன்பாடு

$\frac{\partial u}{\partial t}=\alpha {\mathrm{\nabla }}^{2}u=\alpha (\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2})$ $=\alpha (u_{xx}+u_{yy}+u_{zz})$

இங்கு

 * u = u(x, y, z, t) என்பது வெப்பச்சார்பு;

• $\frac{\partial u}{\partial t}$ என்பது வெப்ப மாறுபாட்டு விகிதம் ;
• u_xx, u_yy, மற்றும் u_zz என்பவை x, y, and z ஆகிய திசையில் அமைந்த வகைக்கெழுக்கள்.