எளிய இசை இயக்கம்

விசையியலிலும் இயற்பியலிலும், எளிய இசையியக்கம் அல்லது தனிச் சீரிசை இயக்கம் என்பது மீள் விசைக்கு இடப்பெயர்ச்சி நேர் விகித சமமாக உள்ள அலைவு இயக்கமாகும்(அதாவது;ஆர்முடுகல் எப்போதும் நிலைத்த புள்ளியை நோக்கி இருக்கும் ). இது சுருளிவில்லின் அலைவு போன்ற பல்வேறு இயக்கங்களின் கணித மாதிரியாக கொள்ளப்படுகிறது. இதைவிட மற்ற இயக்கங்களான ஒரு எளிய ஊசலின் இயக்கம் மற்றும் மூலக்கூறு அதிர்வு போன்றவற்றையும் ஏறக்குறைய எளிய இசையியக்கமாக கொள்ளலாம். ஹூக் இன் விதிக்கு ஏற்ப மீள்விசைக்கு உள்ளாகும் சுருளிவில்லில் உள்ள ஒரு திணிவின் இயக்கத்தை எளிய இசையியக்கமாக வகைகுறிக்கலாம். எளிய இசை இயக்கம் நேரத்துடன் சைன் வளையியாகவும் ஒரேயொரு ஒத்ததிர்வு அதிர்வெண்னைக் கொண்டதாகவும் உள்ளது. எளிய இசையியக்கமானது மிகவும் சிக்கலான இயக்கத்தை ஃபோரியர் பகுப்பாய்வு நுட்பங்கள் மூலம் வகைப்படுத்த ஒரு அடிப்படையை வழங்குகிறது.

முன்னுரை

இங்கு எளிய இசையியக்கமானது உண்மைவெளிலும் தறுவாய்வெளியிலும் காட்டப்படுகிறது. சுற்றுப்பாதை காலக்கிரமமாக உள்ளது. (இங்கு வேக மற்றும் நிலை அச்சுகள் வரைபடங்களை-நேர்ப்படுத்தும் பொருட்டு தரநிலை நடைமுறையில் இருந்து தலைகீழாக உள்ளது)

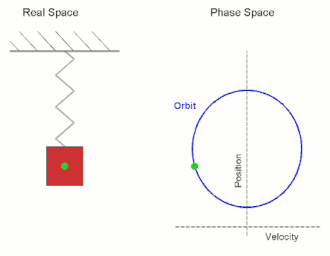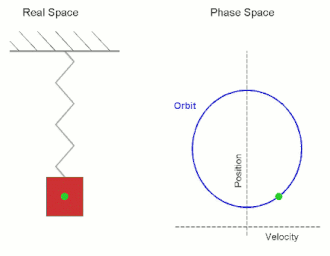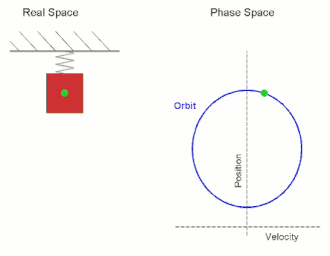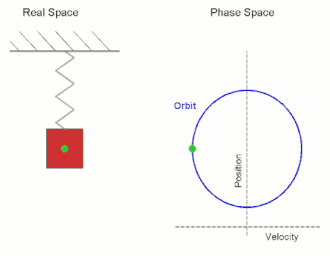
ஒரு எளிய இசை அலையி சுருளி வில்லில் இணைக்கப்பட்டுள்ளது, சுருளி வில்லின் மற்ற முனை சுவர் போன்ற ஒரு உறுதியான ஆதரவுடன் இணைக்கப்பட்டுள்ளது. அமைப்பு சமநிலைத்தானத்தில் ஓய்வில் இருந்தால் அங்கே நிகர விசை இல்லை ஆனால் திணிவு சமநிலைத் தானத்தில் இருந்து இடம்பெயர்ந்தால் ஒர் மீள்விசை சுருளிவில்லில் இருந்து ஹூக்கின் விதிக்கமைய பிறப்பிக்கப்படும். கணிதப்படி, மீள்விசை F பின்வருமாறு

$𝐅=-k𝐱,$

இங்கே F சுருளிவில்லினால் உண்டாக்கப்படும் மீள்விசையாகும் (SI அலகுகளில்: N),K என்பது வில் மாறிலி (N·m⁻¹) மற்றும் x சமநிலை நிலையில் இருந்தான இடப்பெயர்ச்சி (m இல்) ஆகும்.

யாதேனும் எளிய இசை அலையிக்கு:

• அமைப்பு அதன் சமநிலைத் தானத்திலிருந்து இடம்பெயர்ந்திருந்தால், ஹூக் விதியின் படியான ஒர் மீள்விசை அமைப்பினை சமநிலைத் தானத்திற்கு திருப்ப முனைகிறது.

திணிவு அதன் சமநிலை நிலையில் இருந்து இடம்பெயர்ந்த பின்பு, அது ஒர் நிகர மீள் விசையை அனுபவிக்கும். இதன் விளைவாக, அது ஆர்முடுகி சமநிலை தானத்திற்கு திரும்பிச் செல்ல ஆரம்பிக்கும். திணிவு சமநிலை தானத்திற்கு நெருக்கமாக நகரும் போது, மீள்விசை குறைகிறது. சமநிலை தானத்தில், நிகர மீள்விசை மறைந்து விடும். எனினும், x = 0 இல், திணிவு மீள்விசை ஏற்படுத்திய கணத்தாக்கு காரணமாக உந்தத்தினை கொண்டிருக்கும். இதனால் திணிவானது சுருளிவில்லை நெருக்கிக்கொண்டு, சமநிலை தானத்தினைக் கடந்து செல்லும். ஒரு நிகர மீள்விசை பிறகு அதன் வேகத்தை குறைத்து ஓய்வுக்கு கொண்டு வரும். அதனால் அது மீண்டும் சமநிலைத் தானத்தினை அடைய முயற்சிக்கும். அமைப்பில் ஆற்றல் இழப்பு இன்றேல் திணிவு தொடர்ந்து இவ்வாறு அலைவுறும். எனவே எளிய இசையியக்கம் கால இயக்கத்தின் ஒரு வகையாகும்.

எளிய இசை இயக்கத்தின் இயக்கவியல்

ஒரு பரிமாண எளிய இசையியக்கத்திற்கு மாறாக் குணகத்துடன் அமைந்த இரண்டாம் படி நேர் சாதாரண வகையீட்டுச் சமன்பாடாகிய இயக்க சமன்பாட்டை நியூட்டனின் இரண்டாம் விதி, ஹூக்கின் விதியைக் கொண்டு பெறமுடியும்.

$F_{net}=m\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}=-kx,$

இங்கு m ஆடலுறும் உடலின் திணிவு, x என்பது சமனிலைத் தானத்திலிருந்தான இடப்பெயர்ச்சி, k வில் மாறிலி.

ஆகவே,

$\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}=-\left(\frac{k}{m}\right)x,$

மேலுள்ள வகையீட்டுச்சமன்பாட்டை தீர்க்கும் போது சைன் சார்பொன்று தீர்வாகப்பெறப்படும்.

$x(t)=c_1\cos \left(\omega t\right)+c_2\sin \left(\omega t\right)=A\cos (\omega t-\phi ),$

இங்கு

$\omega =\sqrt{\frac{k}{m}},$

$A=\sqrt{{c_1}^2+{c_2}^2},$

$\tan \phi =\left(\frac{c_2}{c_1}\right),$

இத்தீர்வில், c₁, c₂ ஆகியன ஆரம்ப நிலையைப் வைத்து தீர்மானிக்கப்படும் இரு மாறிலிகள், and the origin is set to be the equilibrium position.வார்ப்புரு:Cref2 A என்பது வீச்சம் (சமனிலைத் தானத்திலிருந்தான அதிகூடிய இடப்பெயர்ச்சி), வார்ப்புரு:Nowrap என்பது கோண அதிர்வெண், φ என்பது தறுவாய்.வார்ப்புரு:Cref2

வகையீட்டு நுண்கணித நுட்பங்களைப் பயன்படுத்தி, திசைவேகம், ஆர்முடுகல் ஆகியவற்றை நேரத்தின் சார்புகளாக கண்டறியலாம்:

$v(t)=\frac{\mathrm{d}x}{\mathrm{d}t}=-A\omega \sin (\omega t+\phi ),$

$a(t)=\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}=-A{\omega }^2\cos (\omega t+\phi ).$

ஆர்முடுகலை இடப்பெயர்ச்சியின் சார்பாக பின்வருமாறு எழுதலாம்:

$a(x)=-{\omega }^{2}x.$

வார்ப்புரு:Nowrap என்பதால்,

$f=\frac{1}{2\pi }\sqrt{\frac{k}{m}},$

வார்ப்புரு:Nowrap என்பதால், (இங்கு T அலைவுகாலம்),

$T=2\pi \sqrt{\frac{m}{k}}.$

இச்சமன்பாடுகள் எளிய இசை இயக்கத்தின் அதிர்வெண்ணும் அலைவுகாலமும் அதன் வீச்சத்திலும் இயக்கத்தின் ஆரம்ப தறுவாயிலும் தங்கியிருக்கவில்லை என்பதை பறைசாற்றுகின்றன.

எளிய இசையியக்கத்தின் ஆற்றல்

t நேரத்தில் தொகுதியின் இயக்க ஆற்றல் K ஆனது

$K(t)=\frac{1}{2}m{v}^2(t)=\frac{1}{2}m{\omega }^2{A}^2{\sin }^2(\omega t-\phi )=\frac{1}{2}k{A}^2{\sin }^2(\omega t-\phi ),$

மற்றும் நிலையாற்றல் U ஆனது

$U(t)=\frac{1}{2}k{x}^2(t)=\frac{1}{2}k{A}^2{\cos }^2(\omega t-\phi ).$

எனவே தொகுதியின் மொத்த பொறிமுறை ஆற்றலானது நிலையான மதிப்பைக் கொண்டிருக்கும்

$E=K+U=\frac{1}{2}k{A}^2.$

உதாரணங்கள்

தடையில்லா சுருளிவில்-திணிவு அமைப்பு எளிய இசையியக்கத்திற்கு உட்படுகிறது.

பின்வரும் பௌதீக அமைப்புக்கள் எளிய இசை அலையியிற்கான சில எடுத்துக்காட்டுக்கள்

சுருளிவில்லில் தொங்கும் திணிவு

k எனும் வில் மாறிலி உடைய சுருளிவில்லில் பொருத்தப்பட்ட திணிவு m எளிய இசையியக்கத்தைக் காட்டும், அதன் சமன்பாடு

$T=2\pi \sqrt{\frac{m}{k}}$

மூலம் அலைவுகாலமானது வீச்சத்திலும் புவியீர்ப்பு ஆர்முடுகலிலும் தங்கியிருக்கவில்லை என்பதைக் அறியலாம்.

சீரான வட்ட இயக்கம்

எளிய இசை இயக்கத்தை சில வேளைகளில் சீரான வட்ட இயக்கத்தின் ஒரு பரிமாண பிரதிபலிப்பாக கொள்ளலாம். பொருளானது ω கோணவேகத்துடன் x-y தளத்தின் உற்பத்திப்புள்ளியை மையமாகக் கொண்ட r ஆரையுடைய வட்டத்தைச் சுற்றி இயங்குமாயின் எந்த அச்சுப்பற்றியும் பொருளின் இயக்கமானது r வீச்சத்தையும் ω கோண அதிர்வெண்ணைக் கொண்ட எளிய இசையியக்கமாக இருக்கும்.

எளிய ஊசலில் தொங்கவிடப்பட்ட திணிவு

தடையில்லா ஊசலின் இயக்கமானது அதன் இழையின் நீளத்துடன் ஒப்பிடுகையில் வீச்சம் மிகச்சிறிதாக இருந்தால் அண்ணளவில் எளிய இசையியக்கமாகக் கொள்ளமுடியும்.

சிறிய கோண அண்ணளவாக்கத்தில், எளிய ஊசலின் இயக்கத்தை அண்ணளவில் எளிய இசையியக்கமாகக் கொள்ளலாம். ℓ நீளத்தில் திணிவொன்று இணைக்கப்பட்டும் g புவியீர்ப்பு ஆர்முடுகலும் உடைய ஊசலின் அலைவுகாலமானது

$T=2\pi \sqrt{\frac{\ell }{g}}$

மெலுள்ள சமன்பாட்டின் மூலம் அலைவுகாலமானது ஊசலின் திணிவிலும் வீச்சத்திலும் தங்கியிருக்கவில்லை என்பதையும் ஆனால் புவியீர்ப்பு ஆர்முடுகலில் (g) தங்கியிருப்பதையும் அறியலாம், ஆகவே அதே நீளமுள்ள ஊசலானது நிலாவில் பூமியிலும் பார்க்க மெதுவாக ஊசலாடும், ஏனெனில் அங்கு ஈர்ப்புப்புலத்தின் வலிமை புவியிலும் குறைவு.

இந்த அண்ணளவாக்கமானது சிறிய கோணங்களிற்கே துல்லியமானதாக இருக்கும், ஏனெனில் கோண ஆர்முடுகல் α அமைவின் சைனிற்கு நேர்விகித சமனாக இருக்கும்:

$mg\ell \sin (\theta )=I\alpha ,$

இங்கு I என்பது சடத்துவத்திருப்பம். θ சிறிதாக இருக்கையில், வார்ப்புரு:Nowrap ஆகவே இக்கணிதக்கூற்று

$-mg\ell \theta =I\alpha$

இது கோண ஆர்முடுகலை θ இற்கு நேர்விகித சமனாக்குகிறது, எளிய இசையியக்கத்திற்கான நிபந்தனையை பூர்த்திசெய்கிறது.

சான்றுகள்

• வார்ப்புரு:Cite book
• வார்ப்புரு:Cite book
• வார்ப்புரு:Cite book
• வார்ப்புரு:Cite book

வெளி இணைப்புகள்

• Simple Harmonic Motion from HyperPhysics
• Java simulation of spring-mass oscillator