வகை நுண்கணிதம்

சார்பின் வரைபடம் கருப்பு நிறத்தில் வரையப்பட்டிருக்கிறது. அந்த சார்புக்கான தொடு கோடு சிவப்பு நிறத்தில் வரையப்பட்டிருக்கிறது. இதில் தொடு கோட்டின் சாய்வானது குறிக்கப்பட்டிருக்கும் புள்ளியில் சார்பின் வகைக்கெழுவுக்குச் சமமாக இருக்கிறது

.

கணிதத்தில் வகை நுண்கணிதம் (differential calculus) என்பது உள்ளீடுகள் மாற்றமடையும் போது சார்புகள் எப்படி மாற்றமடைகினறன என்பதுடன் தொடர்புடைய நுண்கணித உட்பிரிவு ஆகும். நுண்கணிதத்தின் இரு பாரம்பரியப் பிரிவுகளுள் ஒன்று வகை நுண்கணிதம். மற்றொரு பிரிவு தொகை நுண்கணிதமாகும்.

வகை நுண்கணிதத்தின் முதன்மையான ஆய்வுப் பொருள் ஒரு சார்பின் வகைக்கெழு, வகையீடு மற்றும் அவற்றின் பயன்பாடுகளாகும். ஒரு குறிப்பிட்ட உள்ளீட்டு மதிப்பிற்கு ஒரு சார்பின் மதிப்பில் ஏற்படும் மாறுவீதத்தை அந்த உள்ளிடு மதிப்பிற்கு அருகிலான சார்பின் வகைக்கெழுவைத் தருகிறது. வகைக்கெழு காணும் செயல்முறை "வகையிடல்" என அழைக்கப்படுகிறது. வடிவவியல் ஈதியாக, ஒரு வரைபடத்தின் மேலமையும் ஒரு புள்ளியில் அவ் வரைபடத்திற்கு வரையப்படும் தொடுகோட்டின் சாய்வானது அப்புள்ளியில் சார்பின் வகைக்கெழுவிற்குச் (வகைக்கெழு இருக்குமானால்) சமம். பொதுவாக, ஒரு மாறியிலமைந்த மெய்-மதிப்புச் சார்புக்கு, ஒரு புள்ளியில் அச் சார்பின் வகைக்கெழுவானது அந்தப் புள்ளியில் அந்தச் சார்புக்கான சிறந்த நேர்கோட்டு தோராயமதிப்பைத் தீர்மானிக்கும். வகையிடல் செயலானது தொகையீட்டுக்கு நேர்மாறான செயல்பாடு என நுண்கணிதத்தின் அடிப்படைத் தேற்றம் குறிப்பிடுகிறது.

வகையீடானது அனைத்து அளவு சார்ந்த துறைகளிலும் பயன்பாடுகளைக் கொண்டிருக்கிறது. இயற்பியலில் ஒரு நகரும் பொருளின் இடப்பெயர்ச்சியின் நேரத்தைப் பொறுத்த வகைக்கெழு அப்பொருளின் திசைவேகமாகும். நேரத்தின் அடிப்படையிலான திசைவேகத்தின் வகைக்கெழு முடுக்கம் ஆகும். ஒரு பொருளின் உந்தத்தின் இயங்குவிசையின் வகைக்கெழு அந்தப் பொருளுக்கு அளிக்கப்படும் விசைக்குச் சமமானதாக இருக்கும் என இயக்கத்துக்கான நியூட்டனின் இரண்டாவது விதி குறிப்பிடுகிறது. வேதி வினையின் வினைவேகம் ஒரு வகைக்கெழு ஆகும். செய்பணி ஆய்வியலில் தொழிற்சாலைகளை வடிவமைக்கவும் பொருட்களைக் கொண்டு செல்லவும் தேவையான வழிமுறைகளை வகைக்கெழுக்கள் அளிக்கின்றன.

சார்பின் மீப்பெருமதிப்புகளையும், மீச்சிறுமதிப்புகளையும் கண்டறிவதற்கு வகைக்கெழுக்கள் பெருமளவில் பயன்படுத்தப்படுகின்றன. வகைக்கெழுக்கள் தொடர்புடைய சமன்பாடுகள் வகையீட்டுச் சமன்பாடுகள் என அழைக்கப்படுகின்றன. வகைக்கெழுக்கள் மற்றும் அதன் பொதுமைப்படுத்தலும் சிக்கலான பகுப்பாய்வு, சார்பலன் பகுப்பாய்வு, வகையீட்டு வடிவவியல், அளவையியல் மற்றும் நுண் இயற்கணிதம் போன்ற கணிதத்தின் பல துறைகளில் பயன்படுத்தப்படுகின்றன.

வகைக்கெழு

$y=f(x)$ என்ற சார்பின் வரைபடம். ஆரஞ்சு நிறக்கோடு $x=a$ என்ற புள்ளியில் வரையப்பட்ட தொடுகோடு.

வெவ்வேறு புள்ளிகளில் ஒரு வகையிடத்தக்க சார்பின் வகைக்கெழு

$y=-2x+13$ இன் வரைபடம்.

$y=x^2$ சமன்பாட்டின் வரைபடத்தில் $(2,4)$ புள்ளியில் வரையப்பட்ட தொடுகோட்டுடன். தொடுகோட்டின் சாய்வு = $4$. (அச்சுகளில் அளவுதிட்டம்: 1:5)

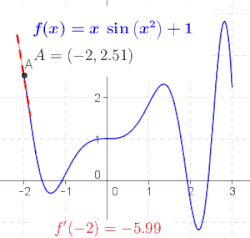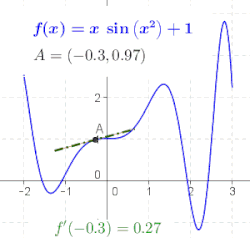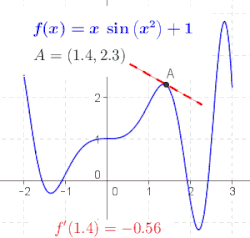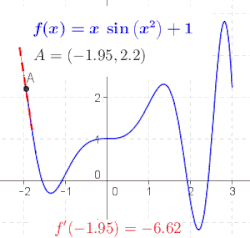
$x=a$ என்ற புள்ளியில் $f(x)$ சார்பின் வகைக்கெழுவானது $(a,f(a))$ என்ற புள்ளியில் சார்பின் வரைபடத்துக்கு வரையப்படும் தொடுகோட்டின் சாய்வாகும். இதனைப் புரிந்துகொள்ள ஒருபடிச் சமன்பாடு ஒன்றின் ($y=mx+b$) சாய்வைக் காணும் முறையைத் தெரிந்து கொள்ள வேண்டும்.

நேர்கோட்டின் சாய்வு (ஒருபடிச் சமன்பாட்டின் சாய்வு)

சாய்வு என்பது சமன்பாட்டின் செங்குத்துத்தன்மையைக் குறிக்கும். ஒருபடிச் சார்பின் ($y=mx+b$) வரைபடமான நேர்கோட்டின் மீது ஏதாவது இரு புள்ளிகளை எடுத்துக்கொண்டு அவற்றின் $x$ மதிப்புகளின் மாற்றத்துக்கு ஏற்றவாறு $y$ இன் மாற்ற அளவைக் கணக்கிட்டு, $y$ இன் மாற்ற அளவை $x$ இன் மாற்ற அளவால் வகுத்தால் நேர்கோட்டின் சாய்வு கிடைக்கும்.

$\text{slope }=\frac{\text{ change in }y}{\text{change in }x}$.

$\frac{\text{change in }y}{\text{change in }x}$ என்பது சுருக்கமாக $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$ என எழுதப்படுகிறது. இதிலுள்ள கிரேக்க எழுத்தான $\mathrm{\Delta }$ என்பது "- இன் மாற்றம்" என்று பொருள்தரும்.

எடுத்துக்காட்டு:

$y=-2x+13$ சமன்பாட்டின் சாய்வு $-2$ (படத்தில் பார்க்க)

$y=x^2$ சமன்பாட்டின் சாய்வு

ஒருபடிச் சமன்பாட்டின் சாய்வு மாறாமல் எல்லாப் புள்ளிகளிலும் சமமாக இருக்கும். ஆனால் $y=x^2$ போன்ற சமன்பாடுகளின் வரைபட வளைகோடுகள் அவற்றின் செங்குத்துத்தன்மையில் மாறுபாடு உடையவை. எனவே ஒருபடிச் சமன்பாட்டின் சாய்வு காணும் முறையை இவற்றுக்குப் பயன்படுத்த முடியாது. அதாவது வரைபடத்தின் மீது ஏதாவது இருபுள்ளிகளை எடுத்துக்கொண்டு அவற்றுக்கான $x$ இன் மாற்ற அளவால் $y$ இன் மாற்ற அளவை வகுத்து சாய்வைக் கணக்கிட முடியாது. இதற்குப் பதிலாக, வரைபடத்தின் ஒரு புள்ளியில் அதன் சாய்வு அப்புள்ளியில் வரையப்படும் தொடுகோட்டின் சாய்வாகக் கொள்ளப்படுகிறது. அதாவது, வரைபட வளைகோட்டின் மீதமையும் ஒரு குறிப்பிட்ட புள்ளியில் வளைகோட்டின் சாய்வானது. அப்புள்ளியில் வளைகோட்டின் தொடுகோட்டின் சாய்வாகும்.

எடுத்துக்காட்டு: $x=2$ புள்ளியில் $y=x^2$ சமன்பாட்டின் சாய்வு $4$. ஏனெனில் $x=2$ புள்ளியில் $y=x^2$ இன் வரைபட வளைகோட்டிற்கு வரையப்படும் தொகோட்டின் சாய்வு $4$

சார்பின் வகைக்கெழு

ஒரு சார்பின் வகைக்கெழுவானது தொடுகோட்டின் சாய்வுக்குச் சமம். தொடுகோடு சார்பின் வரைபடத்தைத் தொடுபுள்ளியில் மட்டுமே தொடும் என்றாலும் வரைபடத்தின் மீது தொடுபுள்ளிக்கு அருகாமையிலமையும் இரு புள்ளிகளை இணைக்கும் வெட்டுக்கோட்டின் தோராயமாகத் தொடுகோட்டைக் கருதலாம். எடுத்துக்கொள்ளப்பட்ட இரு புள்ளிகளும் ஒன்றுக்கொன்று ஒருங்குமளவிற்கு மிகமிக அருகாக நெருங்கும் சூழலில் வெட்டுக்கோடானது தொடுகோடாக தோராயப்படும். இந்நிலையில் வெட்டுக்கோட்டின் சாய்வானது தொடுகோட்டின் சாய்வாகவும் இருக்கும்.

பட விளக்கம்:

$y=x^2$ வளைவரைமீது $(2,4),$ $(3,9)$ புள்ளிகளின் வழியே வரையப்பட்டுள்ள இடைப்புள்ளியிட்ட கோடானது வெட்டுக்கோட்டைக் காட்டுகிறது. இப்புள்ளிகள் ஒன்றுக்கொன்று மிக அருகிலுள்ளதால் வெட்டுக்கோட்டின் சாய்வும் தொடுகோட்டின் சாய்வும் தோராயமாகச் சமம். புள்ளிகள் ஒன்றிணையும் நிலையில் சாய்வுகளின் தோராயப் பிழை மிகமிகக் குறைவானதாக இருக்கும்.

வெட்டுக்கோட்டை பயன்படுத்தினால் சாய்வை நேரிடையாகக் கணக்கிட முடியும். $(x,f(x)),$ $(x+\mathrm{\Delta }x,f(x+\mathrm{\Delta }x))$ ஆகிய இரு புள்ளிகள் வரைபடத்தின் மீது உள்ளவை. இங்கு $\mathrm{\Delta }x$ என்பது மிகச்சிறிய எண்ணைக் குறிக்கும். இவ்விரு புள்ளிகளின் வழியே செல்லும் கோட்டின் சாய்வை $\text{slope }=\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$ வாய்பாட்டின் மூலம் கணக்கிட:

$\text{slope}=\frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x}$

$\mathrm{\Delta }x$ இன் மதிப்பு $0$ ஐ நெருங்க, நெருங்க, இரு புள்ளிகளின் வழியே செல்லும் வரைபடத்தின் வெட்டுக்கோடானது தொடுகோடாக மாறும். எனவே அப்போது வெட்டுக்கோட்டின் சாய்வானது தொடுகோட்டின் சாய்வாகும். இதனை பின்வருமாறு முறைப்படுத்தி எழுதலாம்:

$\underset{\mathrm{\Delta }x\to 0}{\lim }\frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x}$

மேலுள்ள முடிவை '$\mathrm{\Delta }x$ இன் மதிப்பு 0 க்கு மிகவருகில் செல்லச் செல்ல, வெட்டுக்கோட்டின் சாய்வானது ஒரு குறிப்பிட்ட மதிப்பை நெருங்குகிறது' எனக் கூறலாம். இவ்வாறு வெட்டுக்கோட்டின் சாய்வு நெருங்கும் மதிப்பானது சார்பு $f(x)$ இன் வகைக்கெழு எனப்படும்; $f(x)$ இன் வகைக்கெழு $f^{\prime }(x)$ எனக் குறிக்கப்படுகிறது. சார்பு $y=f(x)$ எனக் குறிக்கப்பட்டால், அதன் வகைக்கெழு $\frac{dy}{dx}$ எனக் குறிக்கப்படுகிறது. இதில் $d$ என்பது மீநுண்ணளவு மாற்றத்தைக் குறிக்கிறது. அதாவது $dx$ என்பது x இன் மீநுண்ணளவு மாற்றத்தைக் குறிக்கும்.வார்ப்புரு:Efn

$y=f(x)$ எனில், $f(x)$ இன் வகைக்கெழு:

$\frac{dy}{dx}=f^{\prime }(x)=\underset{\mathrm{\Delta }x\to 0}{\lim }\frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x}$ (இவ்வெல்லை மதிப்பு காணக்கூடியதாக இருக்குமானால்).

இவ்வாறு ஒரு சார்பின் வகைக்கெழுவானது தொடுகோட்டின் சாய்வு என்ற பொருளில் முறையாக வரையறுக்கப்படுகிறது. மேலேதரப்பட்டுள்ள வரையறைப்படி ஒரு சார்பை வகையிடுவது "முதல் கொள்கையிலிருந்து வகையிடல்" என அழைக்கப்படுகிறது.

$y=x^2$ சார்பின் வகைக்கெழு $2x$ என்பதை முதல் கொள்கையிருந்து வகையிடல் முறையில் பின்வருமாறு நிறுவலாம்:

$\begin{array}{cc}\frac{dy}{dx}& =\underset{\mathrm{\Delta }x\to 0}{\lim }\frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x}\\ & =\underset{\mathrm{\Delta }x\to 0}{\lim }\frac{(x+\mathrm{\Delta }x{)}^2-x^2}{\mathrm{\Delta }x}\\ & =\underset{\mathrm{\Delta }x\to 0}{\lim }\frac{x^2+2x\mathrm{\Delta }x+(\mathrm{\Delta }x{)}^2-x^2}{\mathrm{\Delta }x}\\ & =\underset{\mathrm{\Delta }x\to 0}{\lim }\frac{2x\mathrm{\Delta }x+(\mathrm{\Delta }x{)}^2}{\mathrm{\Delta }x}\\ & =\underset{\mathrm{\Delta }x\to 0}{\lim }2x+\mathrm{\Delta }x\\ \end{array}$

$\mathrm{\Delta }x$ இன் மதிப்பு $0$ ஐ நெருங்கும்போது, $2x+\mathrm{\Delta }x$ இன் மதிப்பு $2x$ ஐ நெருங்கும். எனவே $\frac{dy}{dx}=2x$ ஆகும்.

இந்த நிறுவலைப் பொதுமைப்படுத்தி $\frac{d(a{x}^n)}{dx}=an{x}^{n-1}$ ($a,$ $n$ மாறிலிகள்) என்பதையும் நிறுவலாம். இம்முடிவு, வகையிடலின் அடுக்கு விதி என அழைக்கப்படும்.

எடுத்துக்காட்டு:

$\frac{d}{dx}(5x^4)=5(4)x^3=20x^3$.

எனினும் பல சார்புகளை பல்லுறுப்புக்கோவை சார்புகளைப் போல எளிதாக வகையிட முடியாது. அடுக்கு விதியைத் தவிர வகையிடலின் சங்கிலி விதி, வகையிடலின் பெருக்கல் விதி, வகையிடலின் வகுத்தல் விதி போன்ற மேலும் பல விதிகளைப் பயன்படுத்திதான் அவற்றை வகையிட முடியும். வகையிடவே முடியாத சார்புகளும் உண்டு. வகையிடக் கூடிய சார்புகள், வகையிடத்தக்கச் சார்புகள் என அழைக்கப்படும்.

வகையிடலின் வரலாறு

தொடுகோடு சார்ந்த வகைக்கெழுவின் கருத்து மிகவும் பழமையானதாகும். இது கிரேக்க வடிவவியலார்களான யூக்ளிடு (பொது காலம் 300), ஆர்க்கமிடிசு (பொது காலம் 287 முதல் 212 வரை) மற்றும் அப்போலோனியஸ் (பொது காலம் 262 முதல் 190 வரை) ஆகியோரிடையே மிகவும் பழக்கமான ஒன்றாக இருந்தது. எனினும் அவை வகைக்கெழுக்கள் மற்றும் தொடுகோடுகளில் பயன்படுத்தப்படுவதற்கு மாறாக பரப்பளவுகள். மற்றும் கன அளவுகளில் முதன்மையாகப் பயன்படுத்தப்பட்டன.

மாற்ற வீதங்களுக்கு நுண்ணளவுகளைப் பயன்படுத்துவதைப் பண்டைய இந்தியக் கணிதத்தில் காணலாம். 500 CEக்கு முன்பே நிலவின் இயக்கத்தை ஆய்வு செய்வதற்காக வானியல் வல்லுநரும் கணிதயியலாளருமான ஆரியபட்டர் (476–550) நுண்ணளவுகளைப் பயன்படுத்தினார். மாற்ற வீதங்களைக் கணக்கிடுவதற்கு நுண்ணளவுகளைப் பயன்படுத்துவதை இரண்டாம் பாஸ்கரர்(1114-1185) கணிசமான அளவுக்கு மேம்படுத்தினார். உண்மையில் வகை நுண்கணிதத்தின் பல அடிப்படை கருத்தமைவுகள், "ரோலின் தேற்றம்" போன்ற அவரது பணிகளில் காணப்படுவதாக வாதிடப்படுகின்றது..

பொருத்தமான முப்படிக்கோவைகளின் பெரும மதிப்பைப் காண்பதன் மூலம், சில முப்படிச் சமன்பாடுகளுக்கு தீர்வு இருப்பதற்கான நிபந்தனைகளை பெர்சிய கணிதவியலாளர் ஷாராஃப் அல்தின் அல்துசி (1135-1213) அவரது நூலில் (Treatise on Equations) தந்திருக்கிறார். எடுத்துக்காட்டாக, வார்ப்புரு:Mvar இன் நேர்ம மதிப்புகளுக்கு, வார்ப்புரு:Math என்ற முப்படிக்கோவையின் மதிப்பு வார்ப்புரு:Math எனும்போது பெருமமாக இருக்கும் என்றும், அதிலிருந்து வார்ப்புரு:Math சமன்பாடானது

• வார்ப்புரு:Math எனும்போது ஒரேயொரு நேர்மத் தீர்வும்
• வார்ப்புரு:Math எனும்போது இரு நேர்மத் தீர்வுகளும் கொண்டிருக்கும் என்ற முடிவையும் அவர் அளித்துள்ளார்.வார்ப்புரு:Sfn ஷாரப் அல்தின் அல்துசி முப்படிக்கோவையின் வகைக்கெழுவைப் பயன்படுத்தியிருக்க வேண்டுமென்று அறிவியலின் வரலாற்றாசிரியரான ரோஷ்டி ரஷெது கருதுகிறார்.வார்ப்புரு:Sfn எனினும் வேறு சிலர் இதனை மறுத்து அவர் வகைக்கெழுவல்லாத வேறு முறைகளைப் பயன்படுத்தியிருக்கலாம் என்று கருதுகின்றனர்.வார்ப்புரு:Sfn இடை மதிப்புத் தேற்றத்தின் ஆரம்பப் பதிப்பானது வானியல் மற்றும் கணிதத்துக்கான கேரளப் பள்ளியைச் சேர்ந்த பரமேஷ்வரரால் (1370–1460) இரண்டாம் பாஸ்கரர் II மீதான அவரது விளக்கவுரையில் முதன் முதலில் விவரிக்கப்பட்டது.

நுண்கணிதத்தின் நவீன மேம்பாட்டுக்கான சிறப்பு ஐசக் நியூட்டன் (1643 – 1727), கோட்பிரீட் லைப்னிட்ஸ்) (1646 – 1716) ஆகிய இருவரையும் சேரும். அவர்கள் வகையிடல் மற்றும் வகைக்கெழுக்களுக்கு அணுகுமுறைகளை வழங்கினர்.குறிப்பாக, வகையீடு மற்றும் தொகையீடு தொடர்புடைய நுண்கணிதத்தின் அடிப்படை தேற்றத்திற்காக அவர்கள் இச்சிறப்பைப் பெற்றனர். இக்கண்டுபிடிப்புகளால் பரப்பளவுகள், கன அளவுகள் காணும் பழைய முறைகள் வழக்கற்றுப் போயின.வார்ப்புரு:Efn மேலும் அப்பழைய வழிமுறைகள் கணிதவியலாளர் இபின் அல் ஹய்தம் காலத்திற்குப் பின் விரிவுபடுத்தப்படவில்லை. நியூட்டன், லீப்நிஸ் இருவருமே வகைக்கெழுக்கள் சார்ந்த அவர்களது உத்திகளுக்காக ஐசக் பேரோ (1630 – 1677), ரெனே டேக்கார்ட் (1596 – 1650), (கிறித்தியான் ஐகன்சு) (1629 – 1695), பிலைசு பாஸ்கல் (1623 – 1662) மற்றும் ஜான் வால்லிஸ் (1616 – 1703) போன்ற கணிதவியலாளர்களின் ஆரம்பகாலப் பணிகளைக் கணிசமாகப் பயன்படுத்திக் கொண்டனர். குறிப்பாக ஐசக் பேரோ வகைக்கெழுக்களின் ஆரம்ப கால மேம்பாட்டிற்காகப் பாராட்டப்படுகிறார். நியூட்டன் வகையீட்டை முதன்முதலில் இயற்பியலில் பயன்படுத்தியதாலும் லைப்னிட்சு இன்றும் பயன்படுத்தப்படும் பெரும்பாலான குறிமுறைகளை முறைப்படுத்தி மேம்படுத்தியதாலும் இருவரும் வகையீட்டின் வரலாற்றில் முக்கிய நபர்களாக நீடிக்கின்றனர்.

17 ஆம் நூற்றாண்டிலிருந்து பல கணிதவியலாளர்கள் வகையீட்டுக் கோட்பாடுகளுக்கு அவர்களது பங்களிப்பை வழங்கியுள்ளனர். 19 ஆம் நூற்றாண்டில் அகுஸ்டின்-லூயி கோசி (1789 – 1857), பேர்னாட் ரீமன் (1826 – 1866), மற்றும் கார்ல் வியர்ஸ்ட்ராஸ் (1815 – 1897) போன்ற கணிதவியலாளர்கள் நுண்கணிதத்தில் அவர்களது வலிமையான தடத்தினைப் பதித்தனர். மேலும் அந்தக் காலகட்டத்தில் வகையீடானது யூக்ளிடிய வெளி மற்றும் சிக்கலெண் தளம் ஆகியவற்றுக்கும் பொதுமைப்படுத்தப்பட்டது.

வகைக்கெழுக்களின் பயன்பாடுகள்

உகமம் காணல்

f என்பது R (அல்லது ஒரு திறந்த இடைவெளி) மீதான வகையிடத்தக்கச் சார்பு மற்றும் x என்பது f இன் இடஞ்சார்ந்த பெருமம் அல்லது [[இடஞ்சார்ந்த சிறுமம் எனக் கொண்டால் x இல் f இன் வகைக்கெழு பூச்சியமாக இருக்கும். அதாவது, f '(x ) = 0 ஆக இருக்கும் புள்ளிகள், மாறுநிலைப் புள்ளிகள் அல்லது நிலைப் புள்ளிகள் (மேலும் x இல் f இன் மதிப்பு மாறுநிலை மதிப்பு என அழைக்கப்படுகிறது) என்று அழைக்கப்படுகின்றன. (இடைவெளியின் எல்லாப்புள்ளிகளிலும் சார்பை வகையிடமுடியாத நிலயில், வகைக்கெழு காணவியலாத புள்ளிகளும் மாறுநிலைப் புள்ளிகள் எனப்படுகின்றன.

மாறாக, f ஐ இருமுறை வகையிட முடியுமென்றால் f இன் மாறுநிலைப் புள்ளி x ஐ இரண்டாவது வகைக்கெழுவைப் பயன்படுத்திக் காணலாம்:

இரண்டாவது வகைக்கெழுவின் மதிப்பு,

• நேர்மறையானதாக இருந்தால் x ஆனது இடஞ்சார்ந்த சிறுமமாக இருக்கும்.
• எதிர்மறையானதாக இருந்தால் x ஆனது இடஞ்சார்ந்த பெருமமாக இருக்கும்.
• இது பூஜ்ஜியமாக இருந்தால் x ஆனது இடஞ்சார்ந்த சிறுமமாகவோ இடஞ்சார்ந்த பெருமமாகவோ அல்லது இரண்டுமற்றதாகவோ இருக்கலாம் (எடுத்துக்காட்டாக f(x)=x³ ஆனது x=0 இல் மாறுநிலைப் புள்ளியைக் கொண்டிருக்கிறது. ஆனால் அது அதில் பெருமமாகவோ சிறுமமாகவோ இல்லை. அதே சமயம் f (x ) = ±x ⁴ ஆனது x = 0 இல் மாறுநிலைப் புள்ளியைக் கொண்டிருக்கின்றன மற்றும் அவற்றில் முறையே சிறுமம் மற்றும் பெருமத்தைக் கொண்டிருக்கின்றன).

இது இரண்டாம் வகைக்கெழுச் சோதனை என்று அழைக்கப்படுகிறது. இதற்கு மாற்றுமுறை, முதல் வகைக்கெழுச் சோதனை என்று அழைக்கப்படுகிறது. முதல் வகைக்கெழுச் சோதனையில் மாறுநிலைப் புள்ளியின் இருபுறமும் f இன் நேர்ம, எதிர்மக் குறியைப் பொறுத்து பெருமம், சிறுமம் தீர்மானிக்கப்படுகிறது.

வகைக்கெழுக்களை எடுத்து மாறுநிலைப் புள்ளிகளுக்காக தீர்வு காண்பது, இடஞ்சார்ந்த மீச்சிறுமதிப்பு அல்லது மீப்பெருமதிப்பினை எளிதாகக் கண்டறிவதற்கான வழியாக இருக்கிறது. இது உகமம் காண்பதில் மிகவும் பயன் நிறைந்ததாக இருக்கும். முகட்டு மதிப்புத் தேற்றம் மூலமாக மூடிய இடைவெளி மீதான தொடர் சார்பானது அவ்விடைவெளியில் ஒரு முறையாவது அதன் மீச்சிறுமதிப்பு மற்றும் மீப்பெருமதிப்பை அடைய வேண்டும். சார்பானது வகையிடத்தக்கதாக இருந்தால் மீச்சிறுமதிப்பு மற்றும் மீப்பெருமதிப்பு ஆகியவை மாறுநிலைப் புள்ளிகள் அல்லது இறுதிப் புள்ளிகளில் மட்டுமே ஏற்படும்.

இது வளைவரை வரைதலிலும் பயன்பாடுகளைக் கொண்டிருக்கிறது. வகையிடத்தக்க சார்பின் இடஞ்சார்ந்த மீச்சிறுமதிப்பு மற்றும் மீப்பெருமதிப்பு கண்டறியப்பட்டவுடன் அது மாறுநிலைப் புள்ளிகளுக்கு இடையில் அதிகரிப்பதாகவோ அல்லது குறைவதாகவோ இருக்கும் என்பதால் வளைவரையின் தோராயமான வரைபடம் கிடைக்கும்.

மாறுபாடுகளின் நுண்கணிதம்

உகமம் காணல் கணக்கிற்கு ஒரு எடுத்துக்காட்டு, மேற்பரப்பின் மீது இரண்டு புள்ளிகளை இணைக்கும் மீச்சிறு வளைகோட்டைக் கண்டறிதல் ஆகும். இதில் அந்த வளைகோடும் அதே மேற்பரப்பில் அமைந்திருக்க வேண்டும். மேற்பரப்பானது தளமாக இருந்தால் இந்த மீச்சிறுவளைகோடு, நேர்கோடாக இருக்கும். ஆனால் மேற்பரப்பானது வளைபரப்பாக இருந்தால், (எடுத்துக்காட்டாக முட்டை வடிவத்தில் இருந்தால்) மீச்சிறு பாதை உடனடியாகத் தெளிவாகத் தெரியாது. இப்பாதைகள் கோள மேற்பரப்பிற்கு உரியவைகள் என அழைக்கப்படுகின்றன. மாறுபாடுகளின் நுண்கணிதத்தின் அடிப்படைக் கணக்குகளில் ஒன்று இவ்வகையான கோளமேற்பரப்புக்கோடுகளைக் கண்டறிதல் ஆகும். வெளியிலமைந்த மூடிய வளைகோட்டுக்குள் நிரப்பக்கூடிய மீச்சிறு மேற்பரப்பைக் கண்டறிதல் மற்றொரு எடுத்துக்காட்டு ஆகும். இந்த மேற்பரப்பு சிறும மேற்பரப்பு (minimal surface) என அழைக்கப்படுகிறது. சிறும மேற்பரப்பையும் மாறுபாடுகளின் நுண்கணிதத்தைப் பயன்படுத்திக் கண்டறியலாம்.

இயற்பியல்

நுண்கணிதமானது இயற்பியலில் மிகவும் இன்றியமையாததாக இருக்கிறது. பெரும்பாலான இயற்பியல் செயல்பாடுகள் வகையீட்டுச் சமன்பாடுகள் மூலம் விளக்கப்படுகின்றன

• திசைவேகம் என்பது ஒரு பொருளின் இடப்பெயர்ச்சியின் வகைக்கெழுவாக (நேரம் சார்ந்து) இருக்கிறது.
• முடுக்கம் என்பது பொருளின் திசைவேகத்தின் வகைக்கெழுவாக (நேரம் சார்ந்து) இருக்கிறது. அதாவது இது அந்தப் பொருளின் இடப்பெயர்ச்சியின் இரண்டாம் வகைக்கெழுவாக (நேரம் சார்ந்து) இருக்கிறது.

எடுத்துக்காட்டாக, பொருளின் நிலை பின்வருமாறு தரப்பட்டால்:

$x(t)=-16t^2+16t+32,$

அந்த பொருளின் திசைவேகம்:

$\dot{x}(t)=x^{\prime }(t)=-32t+16,$

அந்தப் பொருளின் முடுக்கம்:

$\ddot{x}(t)=x^{″}(t)=-32,$

வகைக்கெழுச் சமன்பாடுகள்

வகைக்கெழுச் சமன்பாடு என்பது சார்புகளின் தொகுப்பு மற்றும் அவற்றின் வகைக்கெழுக்களுக்கு இடையில் உள்ள தொடர்பு ஆகும். ஒரு சாதாரண வகைக்கெழுச் சமன்பாடு என்பது ஒரு மாறியிலமைந்த சார்புகளை அந்த மாறியின் சார்பாக அவற்றின் வகைக்கெழுக்களுடன் தொடர்புபடுத்தும் வகைக்கெழுச் சமன்பாடு ஆகும். ஒரு பகுதி வகைக்கெழுச் சமன்பாடு என்பது ஒன்றுக்கு மேற்பட்ட மாறிகளின் சார்புகளை அவற்றின் பகுதி வகைக்கெழுக்களுக்குத் தொடர்புபடுத்தும் வகைக்கெழுச் சமன்பாடு ஆகும். வகைக்கெழுச் சமன்பாடுகள் இயற்பியல் அறிவியல்கள், கணித மாதிரியமைத்தல் மற்றும் கணிதத்தின் உட்பிரிவுகள் ஆகியவற்றில் இயல்பாக ஏற்படுகின்றன.

எடுத்துக்காட்டாக முடுக்கம், விசை இரண்டுக்கும் இடையில் உள்ள தொடர்பை விவரிக்கும் நியூட்டனின் இரண்டாம் விதியை சாதாரண வகைக்கெழுச் சமன்பாடாகக் குறிப்பிட இயலும்:

$F(t)=m\frac{d^{2}x}{d{t}^2}.$

ஒரு நேரான தடியின் ஊடாக எப்படி வெப்பம் பரவுகிறது என்பதை விவரிக்கும் ஒரு வெளி மாறியிலுள்ள வெப்பச் சமன்பாடு பகுதியளவு வகைக்கெழுச் சமன்பாடு ஆகும்

$\frac{\partial u}{\partial t}=\alpha \frac{{\partial }^{2}u}{\partial x^2}.$

இங்கு u (x , t ) என்பது x நிலை மற்றும் t நேரத்தில் தடியின் வெப்பநிலை ஆகும். α என்பது தடியின் வழியாக எவ்வளவு வேகமாக வெப்பம் பரவுகிறது என்பது சார்ந்த மாறிலி ஆகும்.

இடை மதிப்புத் தேற்றம்

இடை மதிப்புத் தேற்றமானது ஒரு சார்பின் மதிப்புகளுக்கும் அதன் வகைக்கெழுவின் மதிப்புகளுக்கும் இடையில் உள்ள தொடர்பைத் தருவதாகும்.

f (x ) என்பது மெய்மதிப்புடைய சார்பு மற்றும் a மற்றும் b என்பவை a < b உடன் கூடிய எண்களாக இருந்தால் (a , f (a )) மற்றும் (b , f (b )) ஆகிய இரண்டு புள்ளிகளுக்கு இடையில் உள்ள சாய்வானது a மற்றும் b என்பனவற்றுக்கு இடையில் உள்ள c எனும் சில புள்ளிகளில் f இன் வரைபட வளைவரையின் தொடுகோட்டின் சாய்வுக்குச் சமமாக இருக்கும் என இடை மதிப்புத் தேற்றம் கூறுகிறது. இதனை வேறு விதத்தில் பின்வருமாறு கூறலாம்:

$f^{\prime }(c)=\frac{f(b)-f(a)}{b-a}.$

நடைமுறையில் இடை மதிப்புத் தேற்றமானது, ஒரு சார்பின் வகைக்கெழுவின் வரையறைகளைக் கொண்டு அச்சார்பைக் கட்டுப்படுத்துகிறது:

எடுத்துக்காட்டாக, f என்பது ஒவ்வொரு புள்ளியிலும் பூச்சியத்திற்குச் சமமாக இருக்கும் வகைக்கெழுவைக் கொண்டிருக்கிறது என்று கருதுக. இதன் பொருள் என்னவென்றால், இதன் தொடுகோடு ஒவ்வொரு புள்ளியிலும் கிடைமட்டமாக இருக்கிறது என்பதாகும். அதனால் சார்பும் கிடைமட்டமாக இருக்க வேண்டும். இடை மதிப்புத் தேற்றமானது இதனை உண்மையெனப் பின்னுள்ளபடி விளக்குகிறது:

f என்ற வளைவரை மீது ஏதேனும் இரண்டு புள்ளிகளுக்கு இடையில் உள்ள சாய்வானது அப்புள்ளிகளுக்கு இடைப்புள்ளி ஒன்றில் f இன் தொடு கோடுகளில் ஒன்றின் சாய்வுடன் சமமானதாக இருக்கும். எடுத்துக்கொள்ளப்பட்ட முடிவின்படி, அனைத்தின் சாய்வுகளும் பூச்சியமாக இருப்பதால். வளைவரையில் ஒரு புள்ளியில் இருந்து மற்றொரு புள்ளிக்குச் செல்லும் கோட்டின் சாய்வும் பூச்சியமாக இருக்கும். இங்கு சார்பானது மேலேயோ கீழேயோ நகராது. எனவே சார்பின் வரைபடம் கிடைமட்டக் கோடாக இருக்க வேண்டும். வகைக்கெழு மீதான மிகவும் சிக்கலான நிலைகள் துல்லியத்தைக் குறைத்தாலும் அச் சார்பு பற்றிய மிகவும் பயனுள்ள தகவல்கள் கிடைக்கவுதவும்.

டெய்லர் பல்லுறுப்புக் கோவைகள் மற்றும் டெய்லர் தொடர்

வகைக்கெழுவானது சிறந்த சாத்தியமுள்ள தொகை தோராயமதிப்பைத் தருகிறது. ஆனால் இந்தத் தோராய மதிப்பானது மூலச் சார்பில் இருந்து மிகவும் மாறுபட்டதாக இருக்கக்கூடும். தோராயமதிப்பை மேம்படுத்த ஒருபடி தோராயமாக்கலுக்குப் பதிலாக இருபடி தோராயமதிப்பை எடுப்பது ஆகும்.

x ₀ என்ற புள்ளியில் மெய்மதிப்புடைய சார்பு f (x ) இன் நேர்பியலாக்கம் என்பது ஒருபடி பல்லுறுப்புக் கோவை a + b (x - x ₀) ஆக இருக்கிறது. மேலும் இதனை இருபடி பல்லுறுப்புக் கோவை a + b (x - x ₀) + c (x - x ₀)² ஆகக் கருதப்படும் போது இது சிறந்த சாத்தியமுள்ள தோராய மதிப்பினைத் தரக்கூடும். முப்படி பல்லுறுப்புக் கோவை a + b (x - x ₀) + c (x - x ₀)² + d (x - x ₀)³ ஆக இருக்கும் போது இன்னும் சிறந்த தீர்வைப் பெறலாம். மேலும் இந்த கருத்து தொடர்ந்து அதிகளவில் பல்லுறுப்புக் கோவைகளை அதிகரித்துக் கொண்டே செல்வதற்கும் பொருந்தும். இந்தப் பல்லுறுப்புக் கோவைகள் ஒவ்வொன்றுக்கும் a, b, c மற்றும் d ஆகிய சிறந்த சாத்தியமுள்ள குணகங்கள் தேர்ந்தெடுக்கப்பட வேண்டும். அப்போதுதான் கிடைக்க்கூடிய சார்பின் தோராயமதிப்பு மிகச் சிறந்த சாத்தியமுள்ள தோராய மதிப்பாக அமையும்.

x ₀ இன் அண்மையகத்தில் aக்கு சிறந்த சாத்தியமுள்ள தேர்வு எப்போதும் f (x ₀) ஆகவும், bக்கு எப்போதும் f' (x ₀) ஆகவும் இருக்கிறது. c, d மற்றும் பிற உயர்நிலை குணகங்களுக்காக இந்த குணகங்கள் f இன் உயர் வகைக்கெழுக்கள் மூலமாக வரையறுக்கப்படலாம். இதில் c எப்போதும் f'' (x ₀)/2 வையும் d எப்போதும் f''' (x ₀)/3! ஐயும் கொண்டிருக்கும். இந்தக் குணகங்களைப் பயன்படுத்தும் போது f இன் டெய்லர் பல்லுறுப்புக் கோவை கிடைக்கும்.

வார்ப்புரு:Math படியுள்ள இன் டெய்லர் பல்லுறுப்புக் கோவையானது வார்ப்புரு:Math இன் சிறந்த தோராயமதிப்பைக் கொடுக்கக்கூடிய வார்ப்புரு:Math படியுள்ள ஒரு பல்லுறுப்புக் கோவையாகும். மேலும் அதன் குணகங்களை மேற்கண்ட வாய்பாடுகளை பொதுமைப்படுத்தல் மூலமாகக் கண்டறியலாம். தோராயமாக்கல் எந்தளவிற்குச் சிறந்ததாக இருக்கிறது என்பதற்கான துல்லியமான வரம்பினை டெய்லரின் தேற்றம் தருகிறது. வார்ப்புரு:Math என்பது வார்ப்புரு:Math க்கு குறைவாயுள்ள அல்லது சமமாகவுள்ள படியின் பல்லுறுப்புக்கோவையாக இருந்தால், வார்ப்புரு:Math படியுள்ள டெய்லர் பல்லுறுப்புக் கோவையானது வார்ப்புரு:Math க்குச் சமமானதாக இருக்கும்.

டெய்லர் பல்லுறுப்புக் கோவைகளின் எல்லையானது "டெய்லர் தொடர்" என்று அழைக்கப்படும் முடிவிலாத் தொடர்கள் ஆகும். பொதுவாக, டெய்லர் தொடர் மூலச் சார்புக்கு மிகவும் சிறந்த தோராயமதிப்பாக இருக்கும். டெய்லர் தொடருக்குச் சமமாக உள்ள சார்புகள் பகுப்புச் சார்புகள் என்று அழைக்கபடுகின்றன. தொடர்ச்சியற்ற சார்புகளும் கூர் முனையுள்ள சார்புகளும் பகுப்புச் சார்புகளாக இருக்க முடியாது; எனினும் பகுப்புச் சார்புகளாக இல்லாத சீரான சார்புகளும் உள்ளன.

உள்ளுறை சார்புத் தேற்றம்

வட்டங்கள் போன்ற சில இயல்பான வடிவியல் வடிவங்களை சார்பின் வரைபடமாக வரைய இயலாது. எடுத்துக்காட்டாக, F (x , y ) = x ² + y ² − 1 என்ற சார்பை எடுத்துக்கொண்டால் வட்டமானது F (x , y ) = 0 ஐ நிறைவு செய்யும் அனைத்து (x , y ) சோடிகளின் கணமாக இருக்கும். இந்தக் கணமானது F இன் பூச்சியக் கணம் என அழைக்கப்படுகிறது. மேலும் வட்டமானது, மூலச் சார்பான F (x , y ) = x ² + y ² − 1 இன் வரைபடம் பரவளையவுருவை ஒத்ததல்ல என்பதையும் காணலாம்.

உள்ளுறைச் சார்புத் தேற்றமானது F (x , y ) = 0 போன்ற தொடர்புகளைச் சார்புகளாக மாற்றம் செய்கிறது. இத்தேற்றத்தின்படி, F சார்பானது தொடர்ந்து வகையிடத்தக்கதாக இருந்தால், பெரும்பாலான புள்ளிகளைச் சுற்றி F இன் பூச்சியக் கணமானது சார்புகளின் வரைபடங்களை ஒன்றாக ஒட்டியதுபோன்று தோன்றும். இவ்வாறில்லாத புள்ளிகள், வார்ப்புரு:Math இன் வகைக்கெழுவின் மீதான ஒரு நிபந்தனையைக் கொண்டு தீர்மானிக்கப்படுகின்றன. எடுத்துக்காட்டாக $\pm \sqrt{1-x^2}$ என்ற இரண்டு சார்புகளின் வரைபடங்களை ஒட்டுவதன் மூலம் வட்டத்தைப் பெறலாம். (-1, 0) மற்றும் (1, 0) தவிர்த்து வட்டத்தின் மீதான ஒவ்வொரு புள்ளியின் அருகாமையில் இவ்விரு சார்புகளில் ஏதேனுமொன்று வட்டத்தையொத்த வரைபடத்தைக் கொண்டிருக்கும்.. (இந்த இரண்டு சார்புகளும் (-1, 0) மற்றும் (1, 0) ஆகிய புள்ளிகளைச் சந்திக்கலாம். ஆனால் அது உள்ளுறைச் சார்பு தேற்றத்தின் மூலமாகப் பொறுப்புறுதி அளிக்கப்படவில்லை.)

உள்ளுறைச் சார்புத் தேற்றமானது நேர்மாறுச் சார்புத் தேற்றத்துடன் மிகவும் நெருங்கிய தொடர்பு கொண்டது.